Fundamental Formula: Standard Deviation, Median, FFG Median, FFG Deviation, Calculator Software

FORMULA, version 8.1, April 22, 2003 (3 WE) ~ Retired 16-bit software.
SuperFormula, version 13.1, January 2011 ~ 32-bit software, supersedes FORMULA.

This Web site is the official and only host of the famed Fundamental Formula of Gambling. The Fundamental Formula of Gambling (a.k.a. FFG) is, by far, the most precise and useful instrument in stochastic, or random, or probabilistic events. Nothing in theory of games is more significant or more precise than FFG. The Fundamental Formula of Gambling calculates one very descriptive parameter: the FFG median. Each and every random event repeats, in at least 50% of the cases, after a number of trials less than or equal to the FFG median.

The Fundamental Formula of Gambling leads also to another precise instrument: the FFG deviation. I found it to be significantly more precise and useful than standard deviation. The standard deviation is viewed as:
1) a statistical parameter of a numerical series;
2) a probability parameter of binomial events.

1) The statistical standard deviation is calculated as the square root of the variance; the variance is the average of the differences from the mean of the series. A data series like 1, 2, 3, 6 has a mean equal to (1+2+3+6)/4 = 3. The differences from the mean are: -2, -1, 0, +3. The variance is: {(-2)^2 + (-1)^2 + 0 + (3^2)}/4 = 14/4 = 3.5. Finally, the standard deviation is equal to the square root of the variance: √(3.5) = 1.87.

One serious problem with the standard deviation as an analytical tool: It is distorted by extreme values (extremely high, or extremely low) in the data series.

Super Formula calculates the statistical standard deviation of any numeric data series. The numbers (small or huge, integer or floating point) are first collected in a file (ASCII or text format). The program also calculates the sum; mean average; minimum and maximum values. The statistical standard deviation validates the binomial (probability) standard deviation. Moreover, the FFG (non-standard) deviation more closely fits real data. The reality follows closely the theoretical laws.

2) The binomial standard deviation applies to events with two outcomes: win or lose. For example, betting on heads in coin tossing can lead to win (the appearance of heads) or loss (the appearance of the opposite; tails, in this case). The binomial standard deviation is calculated by the following formula:
Standard deviation = SQR{(N*p*(1-p)}
where p is the probability of appearance and N represents the number of trials, SQR being the programming function of Square root or radical √.

Suppose we toss a coin 100 times (N = 100). The probability of heads is p = 1/2 = .5. The standard deviation is Square root of{100 * 0.5 * 0.5} = √(100 * .25) = Square root of(25) = 5. The expected number of heads in 100 tosses is 0.5 * 100 = 50. The rule of normal probability proves that in 68.2% of the cases, the number of heads will fall within one standard deviation from the number of expected successes (50). That is, if we repeat 1000 times the event of tossing a coin 100 times, in 682 cases we'll encounter a number of heads between 45 and 55.

This Web site offers great probability and statistics software to do a multitude of calculations on the topic of Fundamental Formula of Gambling. They are bundled in a scientific software collection known world over as Scientia.

• The main piece of software is Super Formula.

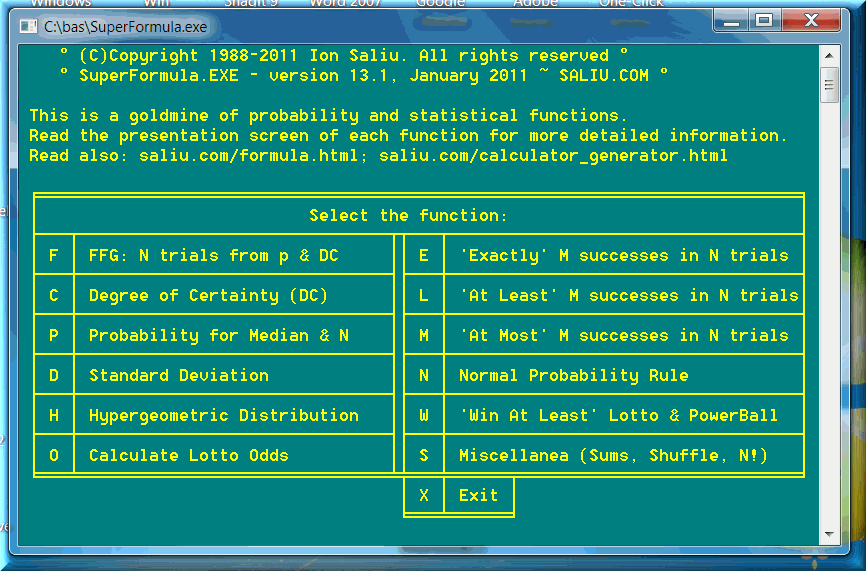
This is the definitive and the ultimate probability, gambling and statistical software. The program boasts several important formulas in theory of probability and statistics:

1) The Fundamental Formula of Gambling (FFG: number of trials from probability p and degree of certainty DC)
2) Degree of Certainty (DC from probability p and number of trials N)
3) Probability of FFG median (probability p from degree of certainty DC and number of trials N)
4) The Binomial Distribution Formula (BDF: EXACTLY M successes in N trials)
5) The Probability of AT LEAST M successes in N trials
6) The Probability of AT MOST M successes in N trials
7) The Probability to WIN AT LEAST 'K of M in P from N' at Lotto & Powerball
8) The Binomial Standard Deviation (BSD)
9) Normal Probability Rule (more precise than Gauss curve)
10) Calculate Lotto Odds, for '0 of k' to 'm of k'
11) Hypergeometric Distribution Applied to Lotto Odds
12) Miscellanea: Sums of numbers, statistical standard deviation, permutations, arrangements, shuffle numbers.

"Standard, standard deviation
Why's so random the Creation?"
"Well… It's All random overall,
Be it straight, crooked, or small;
For there is no Perfect Shape,
Be it rock, river, or grape!"
(The Hymn of Universal Randomness, the Fundamental Rule of the Universe)

Resources in Theory of Probability, Mathematics, Statistics, Standard Deviation, Software

• The Best Introduction to Standard Deviation: Theory, Algorithm, Software.

• The Latest on: Standard Deviation, Variance, Fluctuation, Volatility, , Variability, Variation, Dispersion, Median, Mean Average.
• Standard Deviation, Gauss, Normal, Binomial, Distribution
  Calculate: Median, degree of certainty, standard deviation, binomial, hypergeometric, average, sums, probabilities, odds.

• FORMULA: Standard deviation, politics.
• Generate combinations inside the bell Gauss curve, around the median.
• Upgrade to FORMULA: Standard deviation, binomial distribution.
• Probability, odds, standard deviation, binomial software.
• Software, formulae to calculate lotto odds, hypergeometric distribution probability.
• Probability, Odds, Formulae, Algorithm, Software Calculator.

• Download Probability, Mathematics, Statistics, Standard Deviation Software.

Comments:
: Standard Deviation, Median, FFG Median, Deviation, Variance, Software. The standard deviation is equal to the square root of the variance. The binomial standard deviation applies to events with two outcomes: win or lose. For example, betting on heads in coin tossing can lead to win (the appearance of heads) or loss (the appearance of the opposite; tails, in this case). The binomial standard deviation is calculated by the following formula: Standard deviation = square root {(N*p*(1-p)}. The rule of normal probability proves that in 68.2% of the cases, the number of heads will fall within one standard deviation from the number of expected successes (50). Standard Deviation: This function calculates the binomial standard deviation for binomial events (i.e., experiments characterized by two and only two outcomes: win or loss; success or failure). This is the theoretical or expected value of the standard deviation. The standard deviation can also be calculated post facto: after the experiment. A lottery filter goes up and down from an average value. The standard deviation calculates the positive average of all deviations (fluctuations) from an average norm. Title: Standard Deviation, Median, Variance, Free Software to Calculate the Standard Deviation. Upgrade to FORMULA software for gambling, probability calculations: statistic and binomial standard deviation, binomial distribution, Gauss curve, normal distribution, variance, median. Read about standard deviation, FFG deviation, median, FFG median, mean, average, binomial, normal distribution. Analysis of probability, software, mathematics, theory of probability, theory of games, statistics, standard deviation, combinations, Gauss, Gauss distribution, Gauss curve, normal distribution curve. Evaluation by normal probability rule, gambling, formula, calculate, calculator; evaluate the standard deviation of data series.