
Mathematics of Combination Sequence Number (CSN) or Lexicographical Order (Index) – Heated Debates
By Ion Saliu, Programmer of Lexicographic Order Software




Published on July 11, 2001 — last update September 2011.
• Apparently, the topic had been discussed for years. One formula was presented in newsgroups, especially rec.gambling.lottery. Many readers, without a deep mathematical analysis, had accepted it. Some still believe in that formula in a religious fashion.
Others put their personal pride above anything, regardless of proof or reasoning. There are situations when personae will not accept even well demonstrated common truths. You will have a hard time trying to convince personae that “10 + 7 = 17 in the decimal numerical system”.
Here are excerpts from newsgroups on the combination sequence number, CSN subject.
"Ion,
My congratulations to you on a terrific little lexicographic program that CORRECTLY calculates the CSN of any lotto number sequence and is also successful in reversing the process. As you point out below, the formula that has been kicking around here for a few years now is flawed and produces incorrect results. I believe it had its origins with an eccentric math "expert" from New Zealand named Don.
In spite of several other contributors (including myself) pointing this out, that formula continues to be trotted out by various people who, for one reason or another, refuse to accept that it is incorrect. Perhaps your efforts will finally put the issue to rest. Thank you for doing so."
Author: Lazarus
In article Pine.BSI.4.05L.10107102321470.24062-100000@shell.golden.net, john Latala says...
"There is another change in NthIndex. The only problem I have with your algorithm is that it's kind of slow on my HP48 calculator. Just running a program which is a simple FOR loop to count from 1 to 14000000 lotto combinations takes a few hours. At least the other algorithms ran in a reasonable time.
At present I have a program that does CSN to set (i.e. {n1 n2 n3 n4 n5 n6}). For going from set to CSN I wrote a program that does a binary search in the CSN set until it hits the right one. It's not fast, about twenty seconds, but it does work."
• Ion Saliu (royalty-name Parpaluck): "Why do you run it on a calculator? What are the PCs for?
As for your binary algorithm to calculate the CSN and vice versa. Is it the same that Royce Penny presented a while ago in the thread One for the math-heads? Please read my reply. Such a lexicographical order algorithm is incorrect IF it doesn't take into account the largest number in the lotto game. Such an algorithm leads to correct results ONLY in the very beginning of lotto sequences.
For example, combination 1 2 3 4 5 6 has an index (CSN) of 1 in all lotto-6 games. Maybe that's why the “CSN formula” was considered correct for that long. But a combination like 1 2 3 4 6 7 has different CSNs in different games. A lotto 49/6 game goes from 1 2 3 4 5 49 to the next combination: 1 2 3 4 6 7. In a lotto 54/6, the combination 1 2 3 4 5 49 is followed by:
1-2-3-4-5-50
then the combination:
As you can see, 1 2 3 4 6 7 has different CSNs (indices) in the two lottery games."
Ion Saliu
Dick Adams -- The Wizard of Odds and sometimes Taxes too.
"C(5,48)+C(5,47)+C(5,46)+C(5,45) + ....
If that doesn't help you nothing will. :)
Dick - Johnny Walker Black Label works much better.
Do you think that I should tell him also that the formula would be:
Royce Penny
• Dear Mr. Vice-President Dick “Quincy” Adams:
With all due respect, Your formulae are utterly incorrect.
Let's think of a simple combination, such as 1 2 3 4 5 8. What is its CSN? An absurd result, for there is no C(0,1), C(1,2), C(2,3), C(3,4), C(4,5); there can be only C(7,6).
Also importantly, the correct lexicographical formula should take into consideration differences in lotto games formats. One fundamental element of a lotto game format is its largest number. Thus, in a lotto 49/6 game, the CSN (combination sequence number) for combination 6 7 16 20 28 47 is 6,991,908 (exactly the mid-point in the combination set). The same combination 6 7 16 20 28 47 has an index (CSN) of 45,148,858 in a lotto 69/6 game (PA lottery). Your formulae do not lead to these results, the only mathematically correct results.
Although not a general-purpose formula, the lexicographic algorithm I presented a few days ago represents the easiest way to calculate the indexes of any lotto combinations. The algorithm is for the BASIC language, but it can be converted to any programming language. I compiled NthIndex with PowerBasic, especially because of increased speed of execution at the command prompt.
Ion Saliu
"Hello Royce and Dick,
I am not a mathematician and so I derived the logic for the code by just studying the data. It does however rely on a short loop and that means processing power. So the purpose of this email is to ask you to please explain the mathematical formulas mentioned as I don't understand the symbolism C(...) etc.
Again my math is very basic ... :)
• I suggest you drink two six packs of beer and then you won't care. For your mental block, I recommend medicinal discovery of the 20th century: Jack Daniels Black Label. Jack Black cures everything except alcoholism and for that you can go on a maintenance dose."
Dick -- The Wizard of Odds and sometimes Taxes too.
Ion -
It is really that simple, unless you have a mental block, which, according to Dick, can be cured instantly with Jack Daniel's Black Label.
Royce Penny (Lotto-King) - Royce Penny's Money Machine
• To His Majesty King Lotto XLIX:
There are "kingdoms" in this world where the pupils are taught the combinatorial mathematics. The very first rule they learn is this:
The number of combinations of any N elements taken 0 at a time is 1. But 0 elements taken N at a time is an absurdity, Super Crocodilule of Axiomatic Pursuits! I don't know if you still keep your school textbooks. I don't! I would like to refer you, however, to a book recognized in all kingdoms. It just deals with numbers. It compiles mathematical knowledge from various times and "kingdoms". The book is Warren Weaver's Lady Luck. It presents combinatorial analyses starting at page 92.
On the other hand, everybody has the right to set new knowledge, including new mathematics. You have a right to design a combinatorial algorithm with the following premise:
I quote you again:
Your indexing formula, however, is still bad:
What is CSN for combination 1 2 3 4 5 8?
According to your formula, CSN = 0 + 0 + 0 + 0 + 0 + C(7,6)+1 = 7 + 1 = 8.
In reality, CSN is 3:
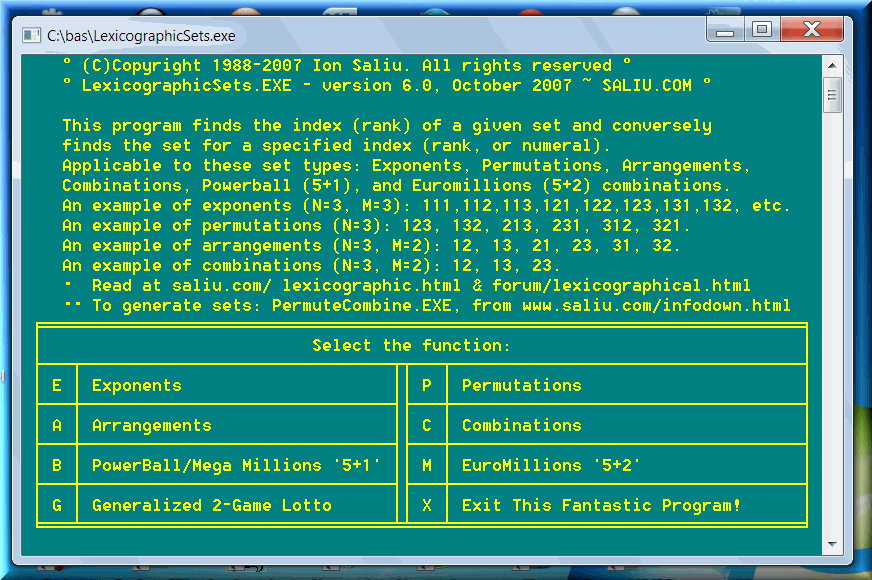
Ultimately, LexicographicSets is the summit of all lexicographic . . . make it lexicographical ordering. The program finds (calculates) the index, or order, or rank, or numeral of all types of sets: exponents, permutations, arrangements, and combinations, including Powerball. Conversely, the program finds (constructs) the set for a given index, or order, or rank, or numeral. The sets are considered in sequential or lexicographic (lexicographical), or dictionary order.
I am afraid whisky in summer time in North America is a no-no. I consider also the divine wine to be a no-no in the hot season. May I recommend Cinzano on ice, with club soda and lemon?
The recipe is known as FFD3: Fundamental Formula of Drinking, the third season. DC in FFD# does not stand for degree of certainty as in FFG. In FFD3, DC stands for Divine Concentration.
À la nôtre! Cheers!
Ion Saliu
This is a comprehensive list of my writings on the topic of lexicographical order or indexing, including algorithms and software.
The following are older and somehow outdated materials I wrote on lexicographical order subjects. Most of the older software is outdated. Nothing (in the whole world) can beat LexicographicSets or DrawIndex. Sentimentalism is good only to a close extent.
Of course, everybody loves to feast on great software, especially when it is free! My combinatorics software (and other categories) is absolutely free to run, for an unlimited period of time. However, only the registered members have a right to download the software. Membership requires a nominal fee — the most reasonable there is to connect to the greatest and most useful lotto software ever created. No kidding! Read the conditions to becoming a registered member: Download Great Software: Paid Membership Required.
Home | Search | New Writings | Software | Odds, Generator | Contents | Forums | Sitemap
-----
1-2-3-4-5-51
1-2-3-4-5-52
1-2-3-4-5-53
1-2-3-4-5-54
1 2 3 4 6 7.
----
CSN = C(n1-1,1)+C(n2-1,2)+C(n3-1,3)+C(n4-1,4)+C(n5-1,5)+C(n6-1,6)+1
where CSN is the Combination Sequence Number?
Or, should I keep it to myself??"
Royce Penny's Money Machine
----
• Your Majesty King Lotto XLIX:
-----
Strange as it apparently seems to some I too use the ID (index or CSN) in my lotto programs. In my attempts to produce a 46,6,3,3,759 lotto wheel, I calculate the ID for any 3 number combination and that helps keep track of which lotto combinations I have already covered. Using this technique and other programming "shortcuts" I have a program which can start producing 26,6,3,3,130 lotto wheels in about an hour.
As per your sig above, there is ”...nothing stronger than reason..." So...the number of sets of 1 number when you have 0 is 0, the number of sets of 2 numbers when you have 1 is 0, the number of sets of 3 numbers when you only have 2 is again 0, the number of sets of 4 numbers with only 3 available is 0, the number of sets of five numbers with only 4 on the table is also zero.
-----
“In combinations of N elements taken M at a time, M must be less than or equal to N.”
For it is absurd to try to combine 2 elements taken them 3 at a time, or 0 elements 6 at a time. If one has only 2 elements, how can one combine 3 of them at a time? Huh? One particular value that M can take is 0. C(N, 0) = 1
“If N is less than M, then the number of combinations is set to 0.”
"So...the number of sets of 1 number when you have 0 is 0, the number of sets of 2 numbers when you have 1 is 0, the number of sets of 3 numbers when you only have 2 is again 0, the number of sets of 4 numbers with only 3 available is 0, the number of sets of five numbers with only 4 on the table is also zero."
CSN = C(n1-1,1)+C(n2-1,2)+C(n3-1,3)+C(n4-1,4)+C(n5-1,5)+C(n6-1,6)+1
1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 5 8 = i.e. CSN = 3.
One empty, tall, clean glass; drop in two cubes of ice; add Cinzano (dry, red vermouth; Martini & Rossi, too) to the half level (DC=50%, also DC=75%); add club soda (or tonic water, or both) to fill-minus-one-finger; add a slice of lemon (or squeeze a lemon) to fill; shake but do not stir. Enjoy! Nothing beats it in summer time in North America!

This is the most intuitive, if not the best, introduction to the apparently difficult concept of lexicographic ordering (or indexing).
This is the most comprehensive and intuitive presentation of the concept of lexicographic ordering (or indexing), including the superior software to tackle the task.
This is how it all started. I responded to challenges in various newsgroups. I came up with the complementary algorithm to the original algorithm by B.P. Buckles and M. Lybanon" (algorithm ACM #515). I offered my lexicographic algorithm bona fide to ACM. A bunch of suckers there tried to make my algorithm look like their creation, not mine!
I expanded the lexicographical index concept to two-in-one games, particularly the U.S. lotto game of Powerball (applicable to Mega Millions as well).
The introduction of DrawIndex, the software that calculates the lexicographic indexes for every combination (draw) in a lotto results file.

