Probability of Predicting NCAA Men's Basketball Brackets with 100% Accuracy

The NCAA Men's Basketball Tournament is known as March Madness. March Madness represents pure Americana, much as blue jeans, automobiles, guns, Oscars…

Investor of great fame Warren Buffett's company, Berkshire Hathaway Inc., is insuring the colossal prize that would go to someone who successfully picks all 64 team brackets in the NCAA men's basketball tournament. The feat is so difficult that the company is betting $1 billion it won't happen.

Axiomatic one, predicting the NCAA Men's Basketball Brackets with 100% accuracy is mission impossible! I am … 100% certain that nobody — but nobody! — has ever predicted the brackets entirely. I did some calculations.

Odds of a perfect NCAA basketball bracket: NIL! Never happened, never will (“Never say never,” said William Faulkner)!

1) If going with the coin toss (p = 1/2) model, the probability is infinitesimal. There are 32+16+8+4+2+1 = 63 games. 2 ^ 63 (2 to the power of 63) = '1 in 9.223372037 * (10^18)' = 0.18 zeroes, then 92233… = 0.00000000000000000092233…

2) If going with the higher odds for some favorite teams, there are still upsets. The #15 seed Florida Gulf Coast upsetting #2 Georgetown would have a probability of 1/100. A #15 going to Sweet 16 would have had a chance very close to 0 (it had never happened before!)

3) For all intents and purposes, the probability to have a perfect bracket is nil, nihil, nada… Even if we have ALL favorites win all the time with an unreal probability of 90% (9/10): the chance is still very low. It would be (9 ^ 63) / (10 ^ 63) = 1.31 *10^60 / 1 * 10^63 = .0013 = 1.3%.

Let's be realistic and alter the theoretical calculations. The college teams are not equally matched in the initiating round.

I worked only with the field of 64 teams (they have now 68, with 8 teams playing a preliminary round). There are 32 games in this newly named Round 2. The compound probability should be 1 in (2 to the power of 32) or 1 in 4,294,967,296 (1 in over 4 billion!) As much parity as they claim in college basketball today, not all teams are equal. Let's say, the aggregate probability (#1) goes down to 1 in (2 to the power of 12) or 1 in 4096. If, luckily, there are 20 games one can predict surely (picking the favorites, that is). That number of failures – 12 – is a reasonable amount of upsets in the newly baptized Round 2.

• The newly named Third Round consists of 16 games. The men's basketball teams are more evenly matched now. Consequently, the number of so-called upsets (when the underdog or the lower seed wins) grows. You should be happy to pick 10 correct results out of 16 matches. The aggregate probability (#2) is 1 in (2 to the power of 6) or 1 in 64.

• The Regional Semifinals (also known as Sweet 16) consists of 8 games. The college basketball teams are much more evenly matched now. Consequently, the amount of so-called upsets (when the underdog or the bigger seed wins) is more unpredictable. You should be happy to pick 5 correct results out of 8 matches. The aggregate probability (#3) is 1 in (2 to the power of 3) or 1 in 8.

• The Regional Finals (also known as The Elite Eight) consist of 4 games. The college basketball teams are much, much more evenly matched now. Consequently, the amount of so-called upsets (when the underdogs win) is much more unpredictable. You should be happy to pick 3 correct results out of 4 matches. The aggregate probability (#4) is 1 in (2 to the power of 1) or 1 in 2.

• The National Semifinals (also known as The Final Four) consist of 2 games. I found this very exciting round to be a 50-50 proposition. The aggregate probability (#5) is 1 in 2.

• Finally, the National Championship! I found this not-always exciting match to be a 50-50 proposition. The aggregate probability (#6) is 1 in 2.

• For the final probability to predict the results of absolutely all games — we multiply the 6 probabilities above.

  4096 * 64 * 8 * 2 * 2 * 2 = 1 in 16,777,216

For one individual: It would take over 16 million editions (years) of March Madness to predict the NCAA brackets with 100% accuracy. Again, this is a statistically modified probability to record perfect NCAA brackets.

The $1 billion challenge has a hugely positive house edge (1,000,000,000 / 16,777,216). By contrast, the traditional lottery has a big negative house edge (from the player's perspective).

On the other hand, there have been hundreds of millions (if not billions) of persons who have filled out the NCAA Men's Basketball Brackets. I've heard of NO absolute success by anybody in this regard. The reason, in my book, must be the bias. People have a favorite team or two; or, people trust too much the seeding of the NCAA selecting committee. Year 2011 was an absolute disaster for the bracket fillers! The Final Four were: #3, #4, #8, and #9! According to the seeding process, The Final Four should be #1, #1, #1, and #1!

In 2012 I did predict 3 of the Final Four, plus the national championship game, plus the national champion. But I missed 25 games! The Dalai Obama missed many more games than yours truly! I posted my predictions in my now-closed forum. But the thread might be still hosted by the WayBack Machine (web.archive.org).

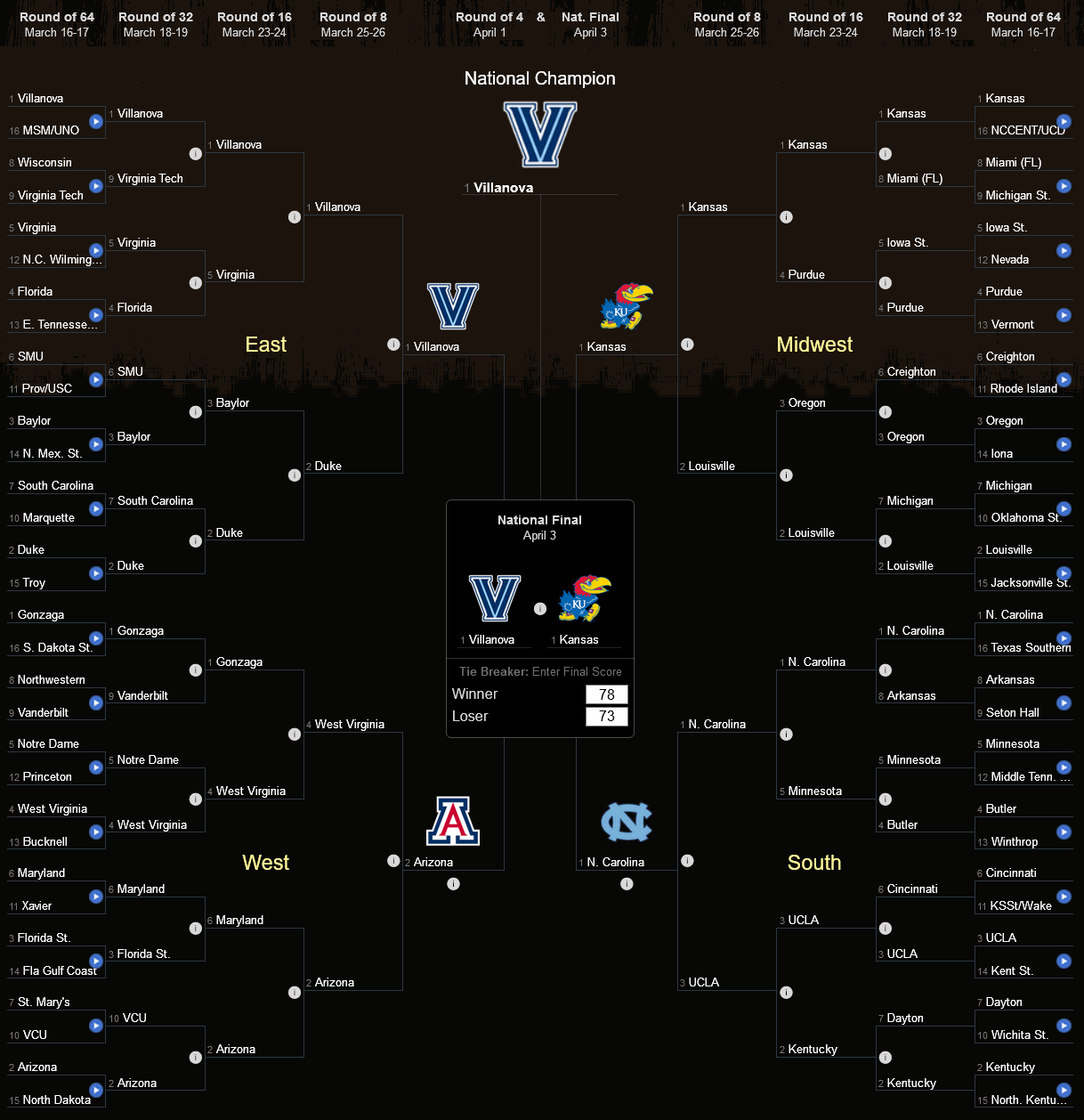
I publish here an image showing how I filled my NCAA brackets (2012). O tempora! O mores!

Tempus fugit! Here is how I filled my bracket at ESPN in the year of grace 2017:

Time flies some more... I filled another bracket at Yahoo Sports in the year of grace 2017. This time around I bet on the favorites more heavily. Some years are characterized by fewer crazy upsets.

4. Resources in Sports Betting: Theory, Mathematics, Excel Spreadsheet, Systems, Parlays

• BrightS: High-Powered Integrated Sports Betting Software.
  It bundles in a convenient system the most important pieces of sports betting software, accompanied by a visual tutorial.

• Results, Performance of SPORTS.XLS, Sports Betting Spreadsheet.
• Winning Combinations Come Predominantly from inside FFG Median Bell.
• Sports Prognosticating, Betting, Excel Spreadsheets.
• Software to Generate 1X2 Systems for Soccer Pools.
• Caveats in Theory of Probability.

• Download Software: Sports Betting, Bet Systems, Excel Spreadsheets, Parlays, 1x2.

For the best mathematical casino gambling strategy (approach) for non-system players, read:
Casino, Casinos: Gambling, Gamble, Win, Winning in Casino.

The Best Casino Gambling Systems: Blackjack, Roulette, Limited Martingale Betting, Progressions:
~ The Fundamental Formula of Gambling and Limited-Step Martingale.

The Best Strategy for Lottery, Gambling, Sports Betting, Horse Racing, Blackjack, Roulette.

Home | Search | New Writings | Odds, Generator | Contents | Forums | Sitemap