
Primer: Probability, Odds, Formulae, Algorithm, Software Calculator
By Ion Saliu, Odds-maker At-Large



Written on September 12, 2002; later updates.
There are many Internet searches on topics such as: odds, probability, calculate odds, software to calculate odds in gambling, lotto odds, lotto probability formulas, etc. Quite a few results point to my web site. The purpose of this page is to better organize the materials on probability and odds.
Probability starts with logic. There is a set of N elements. We can define a sub-set of n favorable elements, where n is less than or equal to N. Probability is defined as the rapport of the favorable cases over total cases, or calculated as:
A simple example of sets and favorable elements: there are 10 balls in a jar; 5 of the 10 balls are red; what is the probability to extract one red ball from the jar? There 5 favorable cases in a total of 10 elements; the probability is 5/10 = ½ = 0.5.
The easiest case is coin tossing. What is the probability of heads in one coin toss: 1 / 2 = 0.5.
The probability can be also understood as expected number of successes in one trial. That formulation makes it easier to understand why probability can never be higher than 1: no event can have more than one success in one try!
There are the tricksters, you know them. ”What if I toss a coin 4 times? Is the probability to get heads equal to 2?” “Hell, no. The probability is still one in two; but the expected number of successes is 2.”
There are many instances when the formulation of probability is reversed and expressed as N-1 to n. This is known as the odds against: the odds against one point face in dice rolling are 5 to 1. The odds against are also expressed as N to n. Some also use the formula n in N to express the so-called favorable odds. I never use this expression, since probability is the correct expression.
It all comes down to calculating the two fundamental elements of the probability formula. I always start with calculating total elements in the set or total possible cases. Then I figure out number of favorable cases. 'Total possible cases' is self-evident sometimes; there are 2 and only 2 cases in coin tossing: heads and tails. The cube has exactly 6 faces. The favorable cases are also easy to figure out. There is one favorable case in coin tossing: either heads OR tails.
Calculating the two fundamental elements of the probability formula is very difficult sometimes. The calculations create a lot of controversy at times. The way we look at the probability or odds can get very tricky. Is it “the odds of EXACTLY n in N” or “the odds of AT LEAST n in N”? In general, there are formulas for calculating the total number of cases and number of possible cases. The binomial distribution probability formula is widely used in instances of “the odds of EXACTLY n in N”. for example, the probability of getting EXACTLY 5 heads in 10 coin tosses is 24.61% or '1 in 4.06'. How about the probability of getting AT LEAST 5 heads in 10 coin tosses? We can no longer use the binomial distribution probability formula in such an instance. Logically, the answer to that challenge is p = ½ = 0.5.
The single-zero roulette game has 37 possible cases (36 numbers, plus 0). The double-zero roulette game has 38 possible cases (36 numbers, plus 0, plus 00). The odds vary with the type of bet. For example, the even-money bet: black/red, odd/even, high/low. There are 18 red numbers and 18 black numbers. The odds are calculated as 18 / 37 = 48.65% or 18 / 38 = 47.37%. The odds are not to be confused with the house edge or house advantage.
At blackjack, the dealer has a 6% advantage because of the simultaneous bust situations. The player plays his/her hand first. As soon as the player busts, the player loses the bet immediately, before the dealer plays her hand. This case of simultaneous bust occurs around 6 times in 100 hands. In other words, the player expects to win 47 hands, while the dealer will win 53 hands. This situation does not consider the basic strategy. The odds from the player's perspective are calculated as 47/100 (47%!) When the basic strategy kicks in, player's winning probability goes all the way to 49.5%, even higher!
There are 1000 total possible cases in pick-3 lottery, the straight bet being considered, from 0 (000, in fact) to 999. Only one 3-digit combination is drawn, therefore the winning probability is 1 / 1000 (0.001). The lottery commission says “the odds are 1 in 1000”, or "1000 to 1”.
There are 10000 total possible cases in pick-4 lottery, the straight bet being considered, from 0 (0000, in fact) to 9999. Only one 4-digit combination is drawn, therefore the winning probability is 1 / 10000 (0.0001). The lottery commission says “the odds are 1 in 10000”, or "10000 to 1”.
Calculating the odds at horseracing is also tricky. We know only statistically that the bettors pick the winner in around 45% of the races. We can also use mathematical formulae to calculate the probability or the odds for certain horseracing wagers. The probability of winning straight trifecta is '1 in N * (N-1) * N(-2)' , where N represents the number of horses in the race. For example: the odds of a straight trifecta in a 12-horse race are '1 in 12 x 11 x 10' = '1 in 1320'. The probability of boxed trifecta is 6 times better; the order of the top three finishers is not important. We can arrange 3 numbers (horses) in 3! = 1x2x3 = 6 ways regardless of order.
The lotto games are much more diverse. The diversity widens when the 'power ball' games are taken into account. The lottery commissions set the odds as exactly k of m. Exactly is the operative word here. I thought it was at least. I started a heated debate in 2001, in newsgroups, thinking that the lottery commissions were dead wrong in their calculations of odds. I admit it, I was wrong, but for a right reason. The odds calculated as at least k of m lead to very different values.
The most certain element in calculating the lotto odds is total possible cases. It is known as total number of combinations C(n, k). The combination formula is widely accepted, expert or not.
or
n! represents the factorial and is calculated as 1*2*3*4*...*n. For example, the lotto 6/49 game has a total of [49 * 48 * 47 * 46 * 45 * 44] / [1 * 2 * 3 * 4 * 5 * 6] = 13,983,816 combinations.
I wrote software to do all probability calculations, fast and accurately:
Scientific Software: Mathematics, statistics, probability, combinatorics, odds, algorithms.
The software in this group is one of the best ever and highly unique. The programs deal with theory of probability; calculating odds for various games of chance, perform statistical functions (e.g. standard deviation, binomial distribution, hypergeometric distribution, etc.) There are also programs that perform tasks in combinatorics. The software calculates and generates permutations, combinations and everything else as far as the number sets are concerned. I bundled all programs in the most powerful package of software for mathematics, probability, statistics: Scientia.
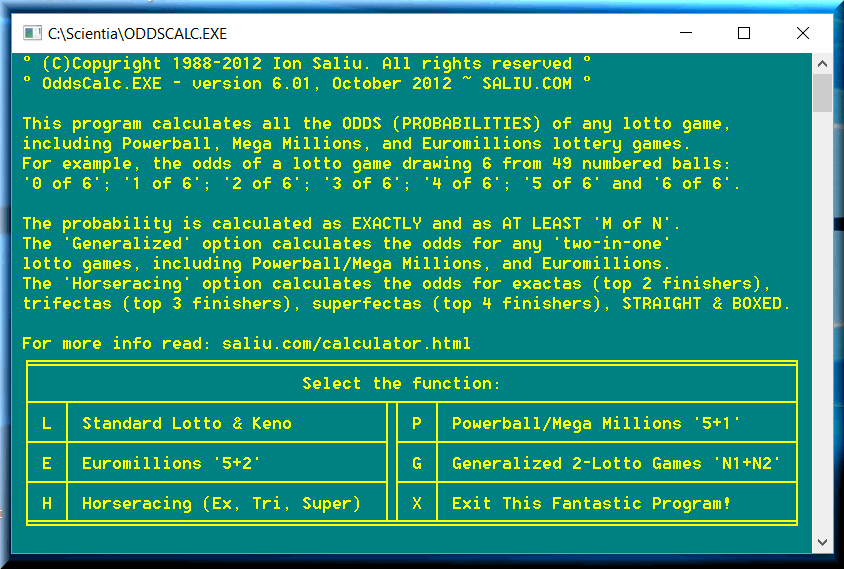
OddsCalc calculates the odds of any lotto game, including power ball and keno. If the game draws 6 winning numbers, the program calculates the odds from '0 of 6' to '6 of 6'. Of course, '6 of 6' represents the jackpot case.
ODDS calculates the lotto odds using the 'hypergeometric distribution probability'. The odds are calculated as 'k of m in n from N'. More clearly, let's suppose a lotto 6/49 game. The lottery draws 6 winning numbers. The player must play exactly 6 numbers per ticket. But the player can choose to play a pool of 10 favorite numbers. What is the probability to get '4 of 6 in 10 from 49'? The odds: '1 in 90'.
See also the resource Random Generator, Odds Calculator in the footer of most Web pages at SALIU.COM.
The page Software, formulae to calculate lotto odds with hypergeometric distribution probability gives more details on calculating the lotto odds for various prizes.


Resources in Theory of Probability, Mathematics, Statistics, Combinatorics, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, statistics, combinatorics, plus software.

Comments:

| Home | Search | New Writings | Odds, Generator | Contents | Forums | Sitemap |
