Blackjack Card Counting Devised by IBM Mathematician Edward O. Thorp Is a Footnote to Gambling History

Posted on August 04, 2000.

In Reply to: Blackjack Card Counting System by Mathematics Professor Edward Thorp posted by Shirley Ann Jennings - SAJA '55 on August 03, 2000.

(SAJA:
Sorry, fata mea, but I still believe you are Chip in travesty! I also think you came up with a soap opera. SAJA is a married woman who wants her anonymity. She is afraid that her husband may turn violent if he finds out that she is the admirer of another man, Chip. Chip is also a friend of the family. They all attend Thorp's card-counting seminaries and lose tons of money in Atlantic City.)

Card counting, as devised by Edward O. Thorp is a footnote to gambling history now. It offered a slight advantage in one-deck games, and especially towards the end of the deck. Ideally, a player could destroy the blackjack game IF knowing the composition of the deck AND the sequence of the remaining cards in the deck. The latter part is the REAL problem: Nobody will ever be able to know the SEQUENCE of the remaining cards in the deck. The count may be +5, but often the sequence is Low card, High card, Low, Low, High, High, Low, Low, High, etc. The dealer has the same probability to get the high cards. It is even more complicated when one considers that there are several blackjack players at the table.

The cards, Low and High, will be distributed randomly among them. What makes a particular player believe he/she would be the one to get the High cards? In one-deck games, and only playing head-to-head against the dealer, there is a slightly higher chance for the player to get a blackjack. The dealer also has an equally higher chance to get a blackjack. The difference is the player is paid 150% for a blackjack, while the dealer always gets 1 to 1 for a natural. Let's say the player has a 2% higher probability to get a blackjack (for a positive count, including Aces).

Under normal circumstances (count = 0, neutral), the probability of a blackjack is just under 5%. What is 2% of 5%? 0.02 x 0.05 = 0.001; that is, 0.1% better probability! That is, a 4.78% chance to get a blackjack, compared to 4.77%. Applying the Fundamental Formula of Gambling to p=4.77% and p=4.78%, we get, approximately, the same median: 14.18 and 14.15 hands. On the average, there will be 14 - 15 hands between blackjacks, in neutral counts, as well as in positive counts. I do not want to enter into the mathematical details of card counting here; see my special Web page in the Resources section.

Suffice to say: The effect of card counting in blackjack is negligible these days. The danger is that most black jack players expect to really win if the count is positive. So, they increase the bet, and keep increasing the bet. The result can be a much faster pace to bankruptcy. Suppose, absurdly, it is true a card-counter has a 2% advantage at blackjack. Does it make sense to play blackjack? The card counter can still lose a lot of money (based on binomial distribution formula). Forget about it!

Finally, once and for all: The predominant report is Thorp was never a successful blackjack player. He was never successful using his card counting system at the blackjack table. The truth is that other famous card counters have failed to gain consistently money in the casino. The famous Ken Uston made money by suing a casino and having been rewarded a million dollars. Kenny made also money by advertising for the casino he "defeated" (the whole legal lawsuit was a farce (read: marketing ploy) aimed at the New York City's huge gambling market). Towards the end of his life, K. Uston made money while working (with numbers, of course!) for oil billionaires of Kuwait. Other card-counting evangelists have made money not at the blackjack table, but by selling their systems, books, "training" materials...

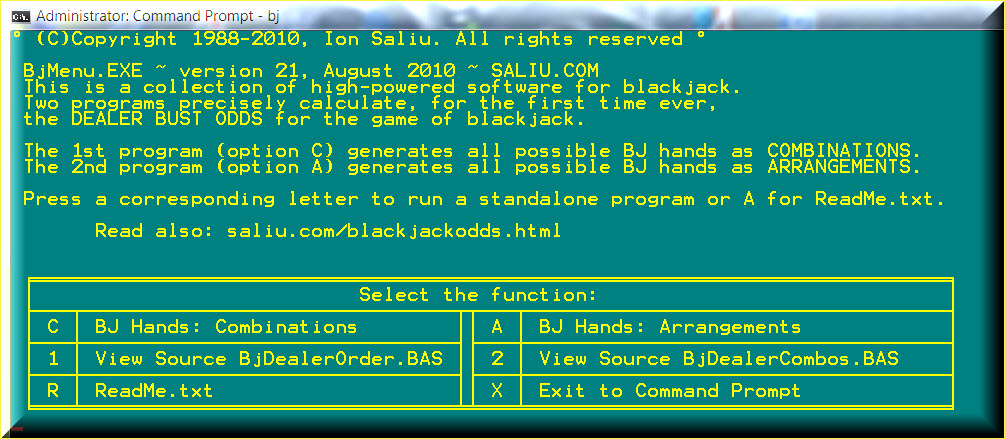
My blackjack software calculates the odds of dealer bust in the most accurate mathematical fashion. We can generate all possible BJ hands mathematically — option A = Arrangements. That is, the order counts. You will notice unmistakably that 10 followed by 6 occurs equally to 6 followed by 10. Even the well-known blackjack basic strategy stands on thin ice. The natural 21 blackjack is equally determined by A + 10 and 10 + A.

Set the record straight on Chip, his real name, criminal behavior, Powerplay roulette, baccarat - June 2004.

Blackjack: Software, Content, Resources, Systems, Basic Strategy, Card Counting

• Blackjack, Black Jack: Basic Strategy, Card Counting; Charts & Tables, Probability, Odds, Software.

• Gambling Mathematics Applied to Blackjack: The Myth and Deception of Blackjack Card Counting .
• Card Counting Blackjack Systems, Reversed Counts, Total Count, All BJ Cards
  Even if counting all blackjack cards in the deck/shoe is no guarantee in beating the game. Permutations, permutations, permutations!

• The Best Blackjack Basic Strategy: Free Cards, Charts.
  All three color-coded charts in one file, in the best decision-making sequence: Split Pairs, to Double Down, to Hit or Stand.

• Download Software: Casino Gambling, Roulette, Blackjack, Baccarat, Craps.

• Casinos React, Counteract if Intelligently Challenged.
• Casinos Intimidate Intelligent Gambling System Authors.

Comments:
: : Blackjack card counting devised by Edward Thorp is a footnote to gambling history now. Card counting, as devised by Edward E. Thorp is a footnote to gambling history now. It offered a slight advantage in one-deck games, and especially towards the end of the deck. Ideally, a player could destroy the blackjack game IF knowing the composition of the deck AND the sequence of the remaining cards in the deck. The latter part is the REAL problem: Nobody will ever be able to know the SEQUENCE of the remaining cards in the deck. The dealer has the same probability to get the high cards. It is even more complicated when one considers that there are several players at the table. The danger is that most blackjack players expect to really win if the count is positive. So, they increase the bet, and keep increasing the bet. The result can be a much faster pace to bankruptcy. Suppose, absurdly, it is true a card-counter has a 2% advantage at blackjack. Does it make sense to play blackjack? The card counter can still lose a lot of money. Wouldn't it be wiser to invest the money in the stock market, or a savings account, or in CD? The investor gets at least 3%-4%, much better in most cases… Thorp was never a successful blackjack player. He was never successful using his card counting system at the blackjack table. The truth is that other famous card counters have failed to gain consistently money in the casino. The famous Ken Uston made money by suing a casino and having been rewarded a million dollars. He made also money by advertising for a casino. Other blackjack card-counting evangelists have made money not at the blackjack table, but by selling their systems or books. Series of countermeasures designed to thwart the Counters the disciples who read Thorp's bestselling Beat the Dealer and tried their own luck with his system. In places where it is legal to ban skilled players from the blackjack action (Las Vega, entire state of Nevada), the casinos commit downright robbery. From what I have read, the casinos show a strong bias towards barring a player when the gambler is at a serious LOSS! I read once that a known card counter was losing some $14,000. Exactly at that point, the pit boss approached the counter and asked him to leave the blackjack game! Of course, the banned player is allowed to play blackjack again. He did work for the casino at the end of his life, but not for the reasons you imply. Parpaluck is simply the greatest blackjack player ever. Title of Ion Saliu's book: "Blackjack card counting devised by IBM mathematician Edward Thorp is footnote to gambling history". Card counting, as devised by Edward E. Thorp is a footnote to gambling history now. It offered a slight advantage in one-deck games, one player against the dealer only, towards the end of card deck. Truths about Edward Thorp, gambling, blackjack, BJ, cards, counting are unfavorable to him. We must consider also penetration, high, low sequences, positive, negative, neutral count, number of decks.