
Standard Deviation: Mathematics, Statistics, Formulas, Software, Algorithms, Equations, Evaluation
★ ★ ★ ★ ★
By Ion Saliu, Formulator of FFG Deviation





1. Introduction to the Concept of Standard Deviation
First capture by the WayBack Machine (web.archive.org) on April 30, 2004.
It started in the American culture with "Computers for Dummies" in the 1980s. I strongly resisted the concept in the very beginning. Then, I realized we all are dummies in most fields of knowledge. If Socrates was right in one and only one thing, it's his assertion "I know that I know nothing." I was a dummy in the field of statistics and standard deviation. Life made me acquire knowledge to handle frequent problems that can be only be solved by knowing, beyond dummy-ness, the deviation in its standard mathematical expression.
So, you, the educated ones in standard deviation, don't curse me for moments that look like a 'standard deviation for dummies' treatment of the topic. Matter of fact, you'll feel like you were a dummy as well, as far as the evaluation of the standard deviation was concerned. You didn't know that before reading this material. It took me years of gambling experiences to come to a clear mathematical evaluation of the standard deviation. The standard deviation of an event (materialized in a data series) is desirable to be under 3 times the median of the series.
The median is a very essential element in randomness and statistical data. I discovered that the median represents the number of trials N for a degree of certainty DC equal to 50%. It is the threshold where possible and impossible are equal. The standard deviation is intimately related to the median, number of trials, and degree of certainty.
Many probability formulas or assessments can be validated with higher degrees of certainty when the standard deviation is below three times the median of the result series. Everything that probability theory says about coin tossing, or throwing the dice, is validated by the standard deviation of mathematically big number experiments.
Also, if data doesn't fit within three standard deviations forget about it! The formula or assessment isn't mathematically valid. The 'Law of big numbers' isn't actually that big. The big numbers are benignly low. Nothing like that scary Infinity! Read Mathematics of Fundamental Formula of Gambling and Ion Saliu's Paradox of N Trials.
In some cultures, the name for variance is "average squared deviation" or "average of squared deviations". The standard deviation becomes "average deviation" or "average of deviations", the absolute (unsigned) values of the deviations being considered. The best measure of random variation, however, is the FFG deviation. You have the chance to learn more about it in my probability book.
The problem with the standard deviation is its huge fluctuation. One and only one term of the series can have an unreasonably big impact on standard deviation. That's why in some judgmental sports they throw out the lowest score and the highest score before calculating the average. It's one simple way of controlling the bias. Moreover, the standard deviation does not indicate the future direction (the short-term trend). Will the next term be higher than the most recent element of data or will we record a decrease?
This author offers this type of evaluation for statistical data as related to the standard deviation.
The data series is uniform (less dispersed, spread), therefore easier to analyze and control, if its standard deviation is less than or equal to the mean average and especially the median.
The data series is volatile (very dispersed, spread), therefore more difficult to analyze and control, if its standard deviation is three times greater than the median and especially the mean average.
The standard deviation is analyzed from two angles:

2. Binomial Standard Deviation
The binomial standard deviation applies to events with two outcomes: win or lose. For example, betting on heads in coin tossing can lead to win (the appearance of heads) or loss (the appearance of the opposite; tails, in this case). The binomial standard deviation is calculated by the following formula:
Standard deviation = Square_Root{(N*p*(1-p)}
That is, the square root of: the number of trials (events) N, multiplied by the probability p, multiplied by the opposite probability (or 1 minus p).
(where: SQR() represents the square root function; p is the probability of appearance and N symbolizes the number of trials).
Suppose we toss a coin 100 times (N=100). The probability of heads is p = 1/2 = 0.5. The standard deviation is SQR{100 * 0.5 * 0.5} = SQR(100 * .25) =SQR(25) = 5. The expected number of heads in 100 tosses is 0.5 * 100 = 50. The rule of normal probability proves that in 68.2% of the cases, the number of heads will fall within one standard deviation from the number of expected successes (50). That is, if we repeat 1000 times the event of tossing a coin 100 times, in 682 cases we'll encounter a number of heads between 45 and 55.

3. Statistical Standard Deviation (in Statistics)
There is no formula to calculate the statistics standard deviation directly (?) That's what they told you in school. That's what they say in other public places with the self-proclaimed goal of education. Only an algorithm can lead to the standard deviation of a data series. Indeed, the algorithm is always available. The following are the steps of the algorithm implemented in my freeware Super Formula. Sum up data; calculate the mean average (sum total divided by the number of elements); deduct each element of the collection from the average; raise each difference to the power of 2; add up the squared differences; divide the new sum total by the number of elements in the data series; the result represents the variance; the square root of the variance represents the famous standard deviation.
A data series like 1, 2, 3, 6 has a mean average (mu) equal to:
μ = (1+2+3+6)/4 = 3.
The differences from the mean are: -2, -1, 0, +3. The variance (sigma squared) is the measurement of the squared deviations. The variance is calculated as:
σ² = {(-2)2 + (-1)2 + 0 + 32}/4=14/4=3.5.
Finally, the standard deviation (sigma) is equal to the positive square root of the variance:
σ = SQR(3.5)=1.87.
Nevertheless, there are formulae (plural, indeed) to calculate the statistical deviation in advance. There is a dominant deviation parameter in all the stochastic (probabilistic) events. In fact, all events are stochastic, since randomness is present in everything-there-is. Nothing-there-is can exist with absolute certainty (see the mathematics of the absurdity of absolute certainty: formula.htm page). The elements of a stochastic phenomenon deviate from one another following mathematical rules. The difference is in the probability of the event (phenomenon). The probability then determines subsequent parameters, such as median, volatility, standard deviation, FFG deviation, etc.
In 2003 I announced that I had discovered a formula for a very important measure in the fluctuation of probability events: FFG deviation. See Lottery Pairing Research. Soon thereafter I have been bombarded with requests to present the formula for FFG deviation and the statistical standard deviation. Of course, I was asked (in strong terms sometimes) to release also free software to accompany the formulae calculations. The requests were also presented in public forums, sometimes strongly worded.
At this time, I do not publish the formulae to calculate the FFG deviation and the statistical standard deviation. Such an act would serve people I do not want to serve. They belong to the following categories: gambling developers and high rollers; lottery systems and software developers; stock traders. I have received many a message from them. They inundated me with correspondence, including postal mail. They would be the ones that would charge serious money out of my effort. The vast majority of people do not really need to know exactly all the formulas involved in standard deviation calculations. Suffice to say that my software does incorporate standard deviation calculations. Also, the greatest random number, combination generator IonSaliuGenerator makes extraordinarily good usage of the standard deviation and deltas (absolute differences between two terms of a series).

4. The Best Software to Calculate or Determine Standard Deviation
You can find here and download great freeware to do a multitude of calculations on the topic of standard deviation, plus theory of probability, and statistics.
Two programs stand out: FORMULA.EXE and SuperFormula.EXE. FORMULA.EXE is 16-bit software, now superseded by SuperFormula.EXE. The latter takes a data file (consisting of real numbers or simulations) and calculates the standard deviation, sum, mean average, median, minimum, and maximum. SuperFormula.EXE has dozens of functions for mathematics, statistics, probability, combinatorics. Read:
Thorough Analysis of Standard Deviation, Variance, Variability, Fluctuation, Volatility, Variation, Dispersion, Median, Mean Average. Function D calculates the binomial standard deviation. The statistical standard deviation is part of option S (Miscellanea), then 2 = Stats of Data (Sum, Standard Deviation, Mean Average, Median, etc.).
The probability or statistical software does not calculate or present directly the formulas for FFG deviation and the statistics standard deviation. But I have written a bundle of computer programs that do such calculations. The standard deviation formulae have been validated for millions of cases, both real-life and simulations. The cases cover very popular probability events such as lotto and lottery, roulette, horseracing, and, yes, stocks! (If a company is not financially sick, the stock fluctuates very closely in accordance to the FFG deviation, like the roulette spins!)
Such software serves a small group of users with strong interests. The software download page presents the terms and conditions for downloading ALL my software.
They are after software like SUMS.EXE. You can download the program from my software downloads site (registered members only).
The application is extraordinarily powerful. It calculates meaningful statistics for a lotto data file: Sum, Root Sum (Fadic Addition), Average, Standard Deviation, Average Deviation from Mean Average, Average of Deltas. At the end of the report, SUMS.EXE calculates the medians of the above statistical parameters. And then they want a lot more: the formulas to calculate in advance the standard deviation, the average of the deviations from the mean, and the average of the deltas.
Here is a sample report for a statistically large data file in the Pennsylvania lotto 5/39 game.
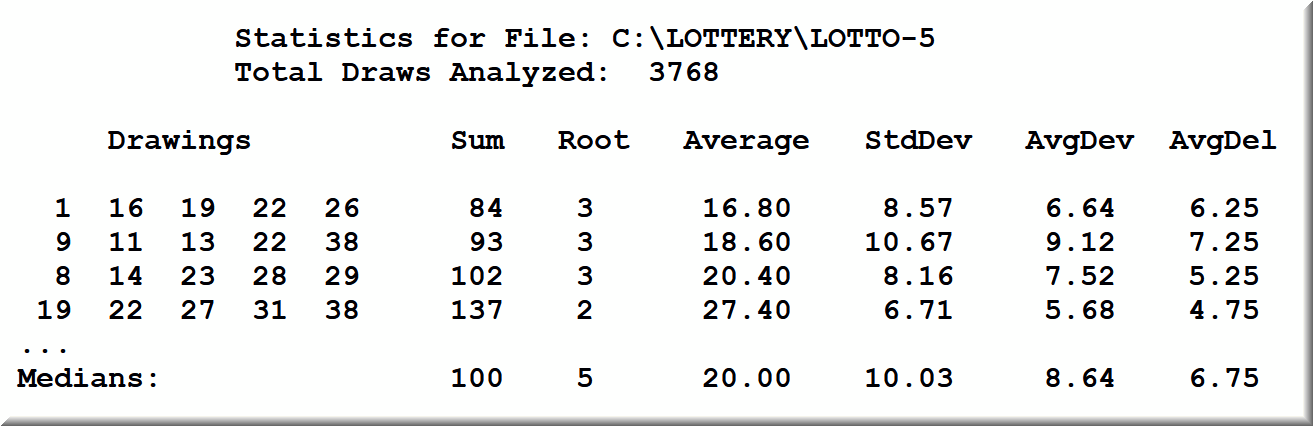
The three fundamental forms of dispersion (deviation):
StdDev = Standard Deviation;
AvgDev = Average Deviation (disregarding the sign);
AvgDel = Average Deltas (absolute differences).
Law: The average of the absolute deviations is always less than the standard deviation. In turn, the average delta is always less than the average deviation and much less than the standard deviation.
Analysis of real-life data must always back the formulae or invalidate formulas. A relation is not a formula if invalidated by data analysis. A rule is not a rule mathematically if data proves just one exception. If things deviate from an established norm, they must do so in accordance to the rules of the watchdog of randomness: Standard Deviation.

 Read Ion Saliu's first book in print: Probability Theory, Live!
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Founded on valuable mathematical discoveries with a wide range of scientific applications, including the organic connection between probability theory and standard deviation the watchdog of randomness.

Resources in Theory of Probability, Mathematics, Statistics, Standard Deviation, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, statistics, standard deviation, plus software.

Home | Search | New Writings | Fundamental Formula | Odds, Generator | Contents | Forums | Sitemap
