Mathematics, Probability: Logarithms of Gambling Formula

Mathematics Of The Fundamental Formula Of Gambling (FFG)
The Authoritative Quintessence Of Gambling Mathematics

By Ion Saliu, Mathematician At-Large

I. The Logic Of The Fundamental Formula Of Gambling
II. The Mathematical Solution: The Divine Logarithm
III. The Mathematics Of The God Concept: The Formula Of Absurdity
• Why God Fears Mathematics, While Einstein Hates Gambling...
IV. Insider Information: It's All In Our Reason
V. Mathematics Of Ion Saliu's Paradox Or Problem Of N Trials
VI. Software: The Divine Tool To Further Empower Reason
VII. Useful Links And Resources Regarding Mathematics

1. The Logical Steps (Algorithm) To The Fundamental Formula Of Gambling

"Let no one enter here who is ignorant of mathematics."
(The frontispiece of Plato's Academy)
"The most important questions of life are, for the most part, really only problems of probability."
(Pierre Simon Marquis de Laplace, "Théorie Analytique des Probabilités")

Here is how I arrived to, by now, famous Fundamental Formula of Gambling (FFG). When laypersons say: "It is so simple!" it always represents undeniable mathematics; therefore, undeniable Truth. I thought I had worked it out on my own, because the formula starts with the very essence of probability theory: p = n/N, reduced to a p = 1/N1. A truth becomes (almost) self–evident when a number of people think INDEPENDENTLY of the same thing. But this human law must be the most undeniable of them all: No Truth is self–evident AND no human thinks totally independently of others!
My first step got my feet wet in my pick 3 lottery software pond. "Probably," that's what I had thought.
I rationalized in this manner. The probability of any 3-digit combination is 1/1000. Therefore, I had expected that the repeat (skip) median of a long series of pick-3 drawings would be 500. It would be similar to coin tossing, where the median of p=1/2 series is 1. In other words, the median of a long series of coin tosses is 1. To my surprise, the repeat median of long series of pick-3 drawings was not 500. It was closer to 700. I checked it for series of 1000 real drawings and also randomly generated drawings. Then I checked the median against series of 10000 (10 thousand) drawings. The median of the skip was always close to 700. Do not confuse it for the median combination in the set. That value of the median is, in fact, either 499 or 500. The correct expression is 4,9,9 or 4 9 9 or 5,0,0 (three separate digits).
What is that median useful for, anyway? Among other properties, the skip median (or median skip) shows that, on the average, a pick-3 combination hits in a number of drawings. Any pick-3 combination hits within 692 drawings in at least 50% of the cases. Equivalently, if you play one pick-3 combination, there is a 50%+ chance it will hit within 692 drawings, or it will repeat no later than 692 drawings. The chance is also (almost) 50% that you will have to wait more than 692 drawings for your number to hit.
I studied theory of probability (gambling mathematics, too!) in high school and in college. Some things get imprinted on our minds. Such information becomes part of our axioms. An axiom is a self-evident truth, a truth that does not necessitate demonstration. We operate with axioms in a manner of automatic thinking.
So, I was analyzing mathematically long pick-3 series, where p=1/1000. Next, I wrote the probability of a single pick-3 number to hit two drawings in a row: p = 1/1000 x 1/1000 = 1/1000000 (1 in 1 million). I have never found useful to work with very, very small numbers in probability.
How about the reverse? The probability of a particular pick-3 number NOT to hit is p = (1 – 1/1000) = 999/1000 = 0.999. This is a very large number. It is almost certain that my pick-3 combination will not hit the very first time I play it.
How about not hitting two times in a row? P = (1 – 1/1000)² = 0.999 to the power of 2 = 0.998. Still, a very large number. I reversed the approach one more time: What is the opposite of not hitting a number of consecutive drawings? It is winning within a number of consecutive drawings.
The knowledge was inside my head. Unconsciously, I used Socrates' dialectical method of “delivering” the truth. (His mother delivered babies.) I also followed steps in De Moivre formula. At this point, I had this relation:
1 – (1 – p)^N
where N represents the number of consecutive drawings.
I thought that for N=500 drawings, the expression above should give the median, or a probability of 50%. So, I calculated 1 – (1 – p)^N = 1 – (1 – 1/1000)⁵⁰⁰ = 1 – (0.999)⁵⁰⁰ = 0.3936 = 39.36%. Thus, my relation became:
0.3936 = 1 – (1 – 1/1000)⁵⁰⁰
I made N = 692. I obtained the value:
1 – (1 – 1/1000)⁶⁹² = 1 - 0.5004 = 49.96% (very close to 50%).
Next step: I made N = 693. I obtained the degree of certainty:
1 – (1 – 1/1000)⁶⁹³ = 1 - 0.4999 = 50.01% (very, very close to 50%).
Thus, the parameter I call the FFG median is between 692 and 693 for the pick 3 lottery.

2. The Mathematical Solution: The Divine Logarithm
I concluded I should not make more assumptions. What if I don't think I know what N should be for the median (50%), or for any other chance, which I simply called the “degree of certainty”? I realized I had the liberty to select whatever degree of certainty I wanted to, and only had to calculate N. The relationship became:
DC = 1 – (1 – p)^N
Then:
(1 – p)^N = 1 – DC
The equation can be solved using logarithms:
log(1 - DC)
N = ----------------
log(1 - p)
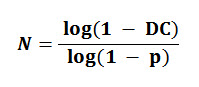
The only unknown is N: the number of consecutive drawings (or trials) that an event of probability p will appear at least once with the degree of certainty DC.
The rest is history. I called the relation “The Fundamental Formula of Gambling” almost automatically. Unintentionally, it might sound cocky. Just refer to it as FFG.
Nothing comes with absolute certainty, but to a degree of certainty! That's mathematics, and that's the only TRUTH.

3. The Mathematics Of The God Concept: The Formula Of Absurdity
Unfortunately, o glorious sons and daughters of Logos and Axioma, the idea of god is a mathematical absurdity! It saddened me first, but we must come to grip with reality. The humans fictionalize because we feel we can't live without the comfort of absolute certainty.
* Some humans with mathematical skills will stumble upon an error, when the degree of certainty DC is set to 100%. There is no absolute certainty in the Universe (or probability equal to 1). It leads to an absurdity: Calculating the number of events necessary for an event of probability p to appear with a degree of certainty equal to 100%. It is absurd. No other qualifications apply, such as “impossible” or “erroneous formula”. Just remember the relation we had before considering the “degree of certainty”. We dealt with “the probability of losing N consecutive times”: (1 – p)^N. In this relation, no N can lead to zero (1 – 100%). Not even 'minus infinite'! A computer program should trap the error and ask the user to enter a DC less than 100% (things like 99.99999999…%).*

Some profound thoughts surrounding this mathematical expression and the false error.
The Fundamental Formula of Gambling (FFG) proves that absolute certainty is a mathematical absurdity. If we set the degree of certainty DC=1 (or 100%), FFG leads to a mathematical absurdity. God is Absolute Certainty, therefore absolute absurdity. I can only imagine de Moivre's reaction when this thought might have crossed his mind: "Certainty is absurd! How can God be True?" It was the 17th century, and the 21st has just a little changed for the better…
Aporia is a special form of absurdity. A Sophist philosopher — Zeno of Elea — constructed a most famous aporia. It is known as the Paradox of Achilles and the tortoise. Read the first philosophical, logical, and mathematical solution: “Zeno Of Elea's Aporia: Achilles Can't Outrun The Tortoise (?)”
It was very easy to apply FFG mathematics to many types of lottery and gambling games. It is at the foundation of several high probability gambling systems I designed: roulette, blackjack, horseracing, and lottery. It works with stocks, too. There is significant randomness in stock evolution. Many stockbrokers came to terms with the reality that all stocks fluctuate in an undeniably random fashion. I am surprised how many brokerage firms have visited my site!

4. Insider Information: It's All In Our Reason
In the year 2001 (1 WE) my memory dug out a real gem. I wrote about it in a post on my message board: Cool stories of the Truth.
“…I found another treasure: A little book in Romanian. Don't they say great things come in small packages? It couldn't be truer than in this case. The book was “The Certainties of Hazard” by French academician Marcel Boll. The book was first published in French in 1941. My 100-page copy was the 1978 Romanian edition. It all came to life, like awakening from a dream. The book presented a table very similar to the table on my “Gambling Formula” page. Then, in small print, the footnote: “The reader who is familiar with logarithms will remark immediately that N is the result of the mathematics formula: N=log(1-pi)/log(1-p).”
That's what I call the Fundamental Formula of Gambling, indeed! Actually, the author, Marcel Boll did not want to take credit for it. Abraham de Moivre largely developed the formula. Then I remembered more clearly about de Moivre and his formula from my school years. Abraham de Moivre himself probably did not want to take credit for the formula. As a matter of fact, the relation only deals with one element: the probability of N consecutive successes (or failures). Everybody knows, that's p^N (p raised to the power of N). It's like an axiom, a self-evident truth. Accordingly, nobody can take credit for an axiom. I thought Pascal deserves the most credit for establishing p = n / N. From there, it's easy to establish p^N. And give birth to so many more worthy numerical relations. For they and everything else are the beloved children of Almighty Number, the ice-cool parent who cares not about children!”

5. Mathematics Of Ion Saliu's Paradox Or Problem Of N Trials
Another look at one of the steps leading to the Fundamental Formula of Gambling:
1 – DC = (1 – p) ^N
We can express the probability as p = 1/N; e.g. the probability of getting one point face when rolling a die is '1 in 6' or p = 1/6; the probability of getting one roulette number is '1 in 38' or p = 1/38. It is common sense that if we repeat the event N times we expect one success. That might be true for an extraordinarily large number of trials. If we repeat the event N times, we are NOT guaranteed to win. If we play roulette 38 consecutive spins, the chance to win is significantly less than 1!
1 – DC = (1 – 1/N)^N
I noticed that (1 – 1/N)^N has a limit. (1 – 1/N)^N = ((N — 1)/N)^N. I reversed and saw more clearly: limit of (N/(N — 1))^N is the definition of e (the base of the natural logarithm). Therefore:
1 – DC =1/e
and
DC = 1 — 1/e
The limit {1 — (1/e)} is approximately 0.63212055...
If the probability is 1/N and we repeat the event N times, the degree of certainty is {1 — (1/e)}, when N tends to infinity. I named this relation Ion Saliu's paradox or problem of N trials.
How long is in the long run? Or, how big is the law of BIG numbers? Ion Saliu's paradox of N trials makes it easy and clear. Let's repeat the number of trials in M multiples of N; e.g. play one roulette number in two series of 38 numbers each. The formula becomes:
1 – DC = (1 – 1/N)^NM = {(1 – 1/N)^N}^M = (1/e)^M
Therefore, the degree of certainty becomes:
DC = 1 – (1/e)^M
If M tends to infinity, (1/e)^M tends to zero, therefore the degree of certainty tends to 1 (certainty, yes, but not in a philosophical sense!). Actually, relatively low values of M make the degree of certainty very, very nearly 100%. For example, if M = 20, DC = 99.9999992%. If M = 50, the PCs of the day calculate DC = 100%. Of course, they can't approximate more than 18 decimal positions! Let's say we want to know how long will it take for all pick-3 combinations come out. The computers say that all 1000 pick-3 combinations will come out within 50,000 drawings with a degree of certainty virtually equal to 100%.
I wrote also software to simulate "Ion Saliu's Paradox of N Trials":
• • OccupancySaliuParadox.EXE version 1.0/November 2004 - Freeware.
Read more on my web page: "Theory of Probability: Best introduction, formulae, algorithms, software".

6. Software: The Divine Tool To Further Empower Reason
I wrote software to handle the Fundamental Formula of Gambling (FFG) and its reverse: Anti-FFG or the Degree of Certainty. There are situations when we want to calculate the Degree of Certainty that an event of probability p will appear at least once within a number of trials N. As a matter of fact, this method offers a more precise correlation between an integer number of trials and a degree of certainty DC expressed as a floating-point number. Furthermore, the program can determine the probability from a data series! The number of elements in the data series is known (N). Sorting the data series can determine the median: The degree of certainty DC equal to 50%!
FORMULA.EXE calculates several mathematical, probability, and statistics functions: Binomial distribution; standard deviation; hypergeometric distribution; odds (probabiulity) for lotto, lottery, and gambling; normal probability rule; sums and mean average; randomization (shuffle); etc.
The program name is FORMULA.EXE, 16-bit DOS software. FORMULA.EXE also calculates the Binomial Distribution Formula (BDF), the Binomial Standard Deviation (BSD), and then some.
• Download the free SuperFormula.EXE (32-bit), FORMULA.EXE, OccupancySaliuParadox.EXE from the FTP downloads site: www.saliu.com/infodown.html.

7. Useful Links And Resources Regarding Mathematics

Theory of Probability: Best introduction, formulae, algorithms, software.
The Birthday Paradox is a particular case of exponential sets (sets with duplicate elements); free software to calculate & generate any form of Birthday Paradox.
Probability: Pairing, couple swapping, hypergeometric distribution.
Mathematics Of The Monty (Monte Hall) Paradox, The Classical Occupancy Problem; More On Ion Saliu's Paradox.
Probability That Player Index N Draws Ticket Number N.
Calculate, generate exponents, permutations (factorial), arrangements, combinations (including Powerball) for any numbers and words.
Pi Day, Pi, Divine Proportion, Golden Proportion, Golden Number, Phi, Fibonacci, Mona Lisa.

The Fundamental Formula of Gambling (FFG) & The Fundamental Table of Gambling (FTG).

Winning lottery, lotto strategies, software.
Winning blackjack strategy, systems, software.
Winning roulette strategy, systems, software.
Winning horse racing strategy, systems, software.
Winning sports betting strategy, systems, software.

The philosophical science of winning.
Almighty Number, Randomness, Universe, God, Order, History, Repetition.
The Fundamental Formula Of Gambling (FFG) may well be the Ultimate Formula of The Everything.

The following pages at this web site offer more special mathematical solutions, functions and formulae, especially in combinatorics. There are algorithms and free software to calculate and generate permutations, exponents, combinations, both for numbers and words. Also, lexicographical order or index can be easily calculated for a large variety of sets.

Lexicographic, lexicographical order, index, ranking, sets: permutations, exponential sets, combinations.
The universal combinations generator for any lotto, Keno, Powerball games: N numbers taken M at a time, in K steps.
Calculate the combination lexicographic order of lotto data files.
Combination Lexicographic Order, Rank, Index: THE Comprehensive and Fast Algorithm.
Index rank lexicographic order lotto combination.
Software for combination algorithm, formula index, ordering.
Combination sequence number or Lexicographic Order Debates.
Combination sequence number or Lexicographic Order: Fast Algorithm.
Combination '1,2,3,4,5,6': Probability and Reality.

Enter your search terms Submit search form

Web www.saliu.com

Subject:
Comments:
: : The Mathematics Of The Fundamental Formula Of Gambling (FFG). The Authoritative Quintessence Of Gambling Mathematics. Let no one enter here who is ignorant of mathematics. The most important questions of life are, for the most part, really only problems of probability. The probability of any 3-digit combination is 1/1000. Therefore, I had expected that the repeat (skip) median of a long series of pick-3 drawings would be 500. It would be similar to coin tossing, where the median of p=1/2 series is 1. In other words, the median of a long series of coin tosses is 1. To my surprise, the repeat median of long series of pick-3 drawings was not 500. It was closer to 700. I checked it for series of 1000 real drawings and also randomly generated drawings. Then I checked the median against series of 10000 (10 thousand) drawings. The median of the skip was always close to 700. We operate with axioms in a manner of automatic thinking. I was analyzing long pick-3 series, where p=1/1000. Next, I wrote the probability of a single pick-3 number to hit two drawings in a row: p = 1/1000 x 1/1000 = 1/1000000 (1 in 1 million). I have never found useful to work with very, very small numbers in probability. The probability of a particular pick-3 number NOT to hit is p = (1 – 1/1000) = 999/1000 = 0.999. It is almost certain that my pick-3 combination will not hit the very first time I play it. How about not hitting two times in a row? What is the opposite of not hitting a number of consecutive drawings? It is winning within a number of consecutive drawings. I thought that for N=500 drawings, the expression above should give the median, or a probability of 50%. What if I do not make assumptions? What if I don't think I know what N should be for the median (50%), or for any other chance, which I simply called the “degree of certainty”? I realized I had the liberty to select whatever degree of certainty I wanted to, and only had to calculate N. The equation can be solved using logarithms: N = log (1 - DC) / log (1 - p). The rest is history. I called the relation "Fundamental Formula of Gambling" almost automatically. Some readers fairly good at mathematics will stumble upon an error, when the degree of certainty is set to 100%. There is no absolute certainty in the Universe (or probability equal to 1). It leads to an absurdity: Calculating the number of events necessary for an event of probability p to appear with a degree of certainty equal to 100%. It is absurd. No other qualifications apply, such as “impossible” or “erroneous formula”. Just remember the relation we had before considering the “degree of certainty”. We dealt with “the probability of losing N consecutive times”: (1 - p) ^ N. In this relation, no N can lead to zero (1 -100%). Not even 'minus infinite'! Some profound thoughts surrounding this mathematical expression and the false error. The Fundamental Formula of Gambling (FFG) proves that absolute certainty is a mathematical absurdity. If we set the degree of certainty DC = 1 (or 100%), FFG leads to a mathematical absurdity. God is Absolute Certainty, therefore absolute absurdity. I can only imagine de Moivre's reaction when this thought might have crossed his mind. It is at the foundation of several high probability gambling systems I designed: roulette, blackjack, horseracing, and lottery. It works with stocks, too. There is significant randomness in stock evolution. Many stockbrokers came to terms with the reality that all stocks fluctuate in an undeniably random fashion. I am surprised how many brokerage firms have visited my site! The Fundamental Formula of Gambling based on solid Mathematical Foundation. It is also the mathematics of God, or proving the inexistence of god mathematically. The book was “The Certainties of Hazard” by French academician Marcel Boll. The book presented a table very similar to the table on my “Gambling Formula” page. Then, in small print, the footnote: "The reader who is familiar with logarithms will remark immediately that N is the result of the formula: N=log(1-pi)/log(1-p)." That's what I call the Fundamental Formula of Gambling, indeed! Actually, the author, Marcel Boll did not want to take credit for it. Abraham de Moivre largely developed the formula. Then I remembered more clearly about de Moivre and his formula from my school years. Abraham de Moivre himself probably did not want to take credit for the formula. Nobody can take credit for an axiom. I thought Pascal deserves the most credit for establishing p = n / N. From there, it's easy to establish p^N. And give birth to so many more worthy numerical relations. Presenting the real Fundamental Formula of Gambling and Ion Saliu paradox. A logarithmic relation started by Abraham de Moivre in eighteenth century. Almighty Number, Randomness, Universe, God, Order, History, Degree of Certainty. The Fundamental Formula Of Gambling (FFG) may well be the Ultimate Formula of The Everything. The following pages at this web site offer more special mathematical solutions, functions and formulae, especially in combinatorics. There are algorithms and free software to calculate and generate permutations, exponents, combinations, both for numbers and words. Presenting Ion Saliu's Paradox Or Problem Of N Trials. Another look at one of the steps leading to the Fundamental Formula of Gambling. The probability of getting one point face when rolling a die is '1 in 6' or p = 1/6; the probability of getting one roulette number is '1 in 38' or p = 1/38. It is common sense that if we repeat the event N times we expect one success. That might be true for an extraordinarily large number of trials. If we repeat the event N times, we are NOT guaranteed to win. If we play roulette 38 consecutive spins, the chance to win is significantly less than 1. I reversed and saw more clearly: limit of (N/(N — 1)) N is the definition of e (the base of the natural logarithm). If the probability is 1/N and we repeat the event N times, the degree of certainty is {1 — (1/e)}, when N tends to infinity. I named this relation Ion Saliu's paradox or problem of N trials. How long is in the long run? Or, how big is the law of BIG numbers? Ion Saliu's paradox of N trials makes it easy and clear. The degree of certainty becomes: If M tends to infinity, (1/e) ^ M tends to zero, therefore the degree of certainty tends to 1 (certainty, yes, but not in a philosophical sense!). Actually, relatively low values of M make the degree of certainty very, very nearly 100%. Within 50,000 drawings with a degree of certainty virtually equal to 100%. All about Gambling, formula, FFG, Abraham de Moivre, Blaise Pascal, Marcel Boll, mathematical, logarithm, logarithms. Study certainty, god, absurd, absurdity, equation, median, probabilities, probability, statistics, combination, combinations. Title: Probability, Mathematics: Logarithms, Formulae of Gambling Mathematics. Science of gambling, formula of degrre of certainty, mathematics, math, formulas, median. Fundamental Formula of Gambling start: de Moivre, Pascal. Mathematical and logical algorithm, algorithms by using logarithm, logarithms. Mathematics of certainty, god, absurd, absurdity. The equation, formula that proves the inexistence of God. More on equation, median, probabilities, probability. Title: Thorough Analysis of Mathematics, Probability, Logarithms of Fundamental Formula Of Gambling (FFG). The Fundamental Formula of Gambling is founded on solid mathematics. It's an undeniable logarithmic relation started by Abraham de Moivre. FFG is the most precise instrument in theory of games. Analyze mathematics, formula, gambling, de Moivre, Pascal, logarithm, logarithms, degree of certainty. Establish the mathematical relation between certainty and god. Discover the formulae of divine absurdity. The equation, probabilities, probability of the everything. Respect the number, numbers, math, maths, formulas, median. Apply probability, consecutive, win, wins, pick 3, casino, horse racing, blackjack - for stock brokers, sports betting, roulette, gambling, formula, mathematics, math, maths, formulas, median, matmatical. The Fundamental Formula of Gambling: Its Mathematical Foundation plus the mathematics of God. Proves the inexistence of god mathematically, not only in a logical manner.

Socrates Home Search Ion, Help! Contact Ion What's New Fundamental Formula of Gambling Probability Theory Combinatorics, Permutations Statistics Software Standard Deviation Lottery, Lotto, Software, Systems Spreadsheets, Lotto, Lottery Blackjack Strategy Roulette Systems Horse Racing Software Sports Betting, Football, Software Baccarat Theory, Software Ion Saliu's Book of Records Random Generator, Odds Calculator Newest Writings Download Free Software Content Categories All Pages, Sitemap

Copyright ©1997-2007, Ion Saliu. All rights reserved worldwide. Reproduction, in any form, of the contents of this site is strictly prohibited. Read important copyright information regarding web site www.saliu.com