


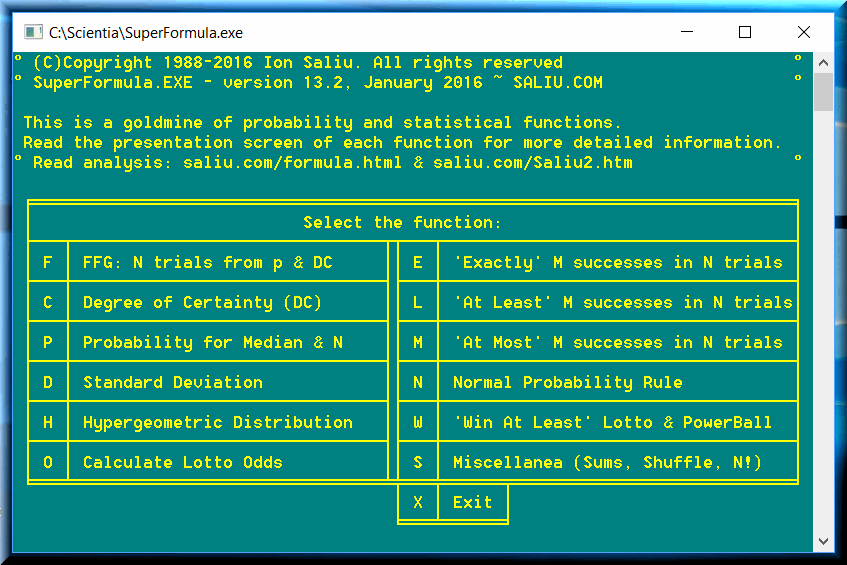
• FORMULA, version 8.1, April 22, 2003 ~ Retired 16-bit software.
• SuperFormula, version 13.1, January 2011 ~ 32-bit software, supersedes FORMULA.
• Shuffle, version 8.0 ~ March 2011.
We may also call it the Fundamental Formula of The Universe or the Formula of The Everything.
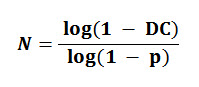
For example, the winning reports created by LotWon software show a series of filters and their medians. If not calculated, you can use an editor such as QEdit and do a column blocking, then sort the column (filter) in descending order. The median represents the middle point of the sorted column. The median also represents the number of SKIPS (trials between hits) for a degree of certainty equal to 50%. I do not describe every filter in my software, so nobody can tell the probability of every filter.
You can determine the odds for a filter using this function of Super Formula. Other filters are described and thus their probabilities can be calculated in advance. They will prove the validity of the Fundamental Formula of Gambling. For example, the probability of 3 of 6 in a 6/49 lotto is 1 in 57. FFG calculates the median for this situation (DC=50%) as 39. Take a real draw history, such as UK 6/49 lotto. Do the winning report for 500 past draws; sort in descending order the filter Threes for layer 1. The median is 37 or closely around 39. Reciprocally, when you see a median equal to 37, you can determine the probability of the parameter as 1 in 54 (very close to the real case of exactly 1 in 57; it is, however, almost equal to at least 1 in 53.nn).
For example, we want to determine the probability of getting exactly 5 heads in 10 tosses. We tossed the coin 7 times and recorded 5 heads. We toss the coin for the 8th time and get another heads (the 6th). We must stop the tossing; the experiment failed. We can no longer get EXACTLY 5 heads in 10 tosses. It is obvious that the previous events influenced the coin toss number 9.
A sequence of events means that the events do not take place at the same time. They occur one after another.
The Binomial Distribution Formula shows some interesting facts. For example, the probability to toss EXACTLY 1 heads in 10 tosses is only 0.98%. It is quite difficult to get only 1 heads and 9 tails in 10 tosses.
The generalized formula for exactly M successes in N trials:
BDF = probability, chance of exactly M successes in N trials;
p = the individual probability of the phenomenon (e.g. p = 0.5 to get heads in coin tossing);
M = the exact number of successes (e.g. exactly 5 tails in 10 coin tosses);
N = the number of trials (e.g. exactly 5 tails in 10 trials).
For example, we want to determine the probability of getting at least 4 heads in 10 tosses. Logically, the following situations qualify as success: 4 heads; 5 heads; 6 heads; 7 heads; 8 heads; 9 heads; and 10 heads. Obviously, the probability is better than the exactly 4 of 10 case.
There is a data type limit. The number of trials N must not be larger than 1754. There will be an overflow if you use very large numbers.
For example, we want to determine the probability of getting at most 4 heads in 10 tosses (no more than 4 in 10). In at least M in N we look at the glass as being half full. Why not look at it from the pessimistic perspective: the glass can be empty sometimes (or present degrees of emptiness)! Logically, the following situations qualify as success: 4 heads; 3 heads; 2 heads; 1 heads; and 0 heads. The probability can be higher than the exactly 4 of 10 or at least 4 of 10 cases, but it won't be better from a player's perspective!
There is a data size limit. The number of trials N must not be larger than 1754. There will be an overflow if you use very large numbers. Blame the permutations (calculated by the factorial operator N!) and the limitations of the computers…
In real life the player gets a better deal, however. The commission does not oblige the players to exactly situations. The real life situation is at least K of M from N. The commissions don't care if you play just 6 numbers, or play a pool of picks. They don't care if you expected 3 of 6 hits, but hit 4 of 6. They'll pay you for the highest prize per ticket. It is clear that at least K of M from N is better than exactly K of M from N from the player's perspective.
If the player plays 57 6-number random picks, the player should expect one 3 of 6 hit. If playing 100 times 57 tickets, the expectation should be 100 3 of 6 hits. Sometimes, however, higher prizes can be hit. That's why the odds of getting at least 3 of 6 from 49 are 1 in 56.66.
Many lotto wheel aficionados might broadcast screams of happiness. Cool down, Wheely! The previous calculations do not imply that 54 lines (combinations) will guarantee 100% in one draw a 3 of 6 49-number wheel! Calculating the minimum number of successes for a 100% guarantee is a totally different matter. It is a book in itself if one considers also the algorithm to generate the successes...
I wrote in the article Fundamental Formula of Wheeling:
“… the probability of winning [exactly] 3 of 6 is 1 in 57. FFG calculates the median for p = 1/57 as 39.16, rounded up to 40 for DC = 50%. How close is that figure (40) to reality in the UK 6/49 history file? The file I've been using for this analysis has 737 draws (contains a few so-called extra draws). The file has 733 regular draws from the beginning of the game to the draw of January 1, 2003. The median for the 3 of 6 case is around 39.”
The calculations are correct, as far as standard deviation is concerned. The FFG median, however is precisely in accordance with the probability of at least 3 of 6: 1 in 56. It's right on the money! Forget about one standard deviation! I had always noticed this small discrepancy in all the data files I analyzed. The filter medians are always a few points lower than the FFG medians. Now it fully makes sense. The medians are the result of at least K of M in N probability, NOT the exactly K of M in N probability!
We may consider from now on the Fundamental Formula of Gambling to be the most precise instrument in games theory. There are a few posts at this web site dealing with Markov chains:
Markov Chains in Lottery, Lotto.
Searching on Markov chains at Google yields close to 100,000 hits! The topic is hot! I stated, however, that FFG outruns Markov by several steps. Again, once and for all, the Fundamental Formula of Gambling is be the most precise instrument in games theory. Unlike Markov chains, FFG considers previous events to be of the essence for future events. The events repeat precisely, according to the famed Fundamental Formula of Gambling.
The binomial standard deviation has great merit. It shows what fluctuation to expect. Before starting the coin toss, one can have an accurate idea of how many heads will fall in a number of trials (tosses). Or how many winning hands one can expect playing 200 blackjack rounds.
The standard deviation for an event of probability
p = .5
in 100 binomial experiments is:
BSD = 5
The expected (theoretical) number of successes is: 50
Based on the Normal Probability Rule:
· 68.2% of the successes will fall within 1 Standard Deviation
from 50 - i.e., between 45 - 55
·· 95.4% of the successes will fall within 2 Standard Deviations
from 50 - i.e., between 40 - 60
··· 99.7% of the successes will fall within 3 Standard Deviations
from 50 - i.e., between 35 - 65.
I have been working thoroughly with pairing strategies, especially in the digit lotteries. I have encountered far better situations than offered by the traditional normal probability rule. That made me to take a different approach to calculating the normal probability rule. The traditional rule is based on Gauss or normal distribution curve. The keyword here is curve, implying continuous. The lottery or gambling are discrete, however. The one size fits all approach leads to discrepancies. In the example above, the new normal probability rule I am using gives:
72.87% of the successes will fall within 1 Standard Deviation
from 0 - i.e., between 45 - 55
One caveat, as in the binomial distribution probability case, there is a data limit: 1500 trials. It covers a pretty good range of lottery and gambling cases.
The probability is calculated as exactly M of N (not at least M of N). Sometimes such probability is 0: the event is impossible; for example 0 of 6 or 1 of 6 for the 6/10 case.
This function handles any type of lotto game, including Keno, Mega Millions, and Powerball. This function incorporates the entire program OddsCalc. The program is still available as standalone, although the integrated Scientia package is highly recommended.
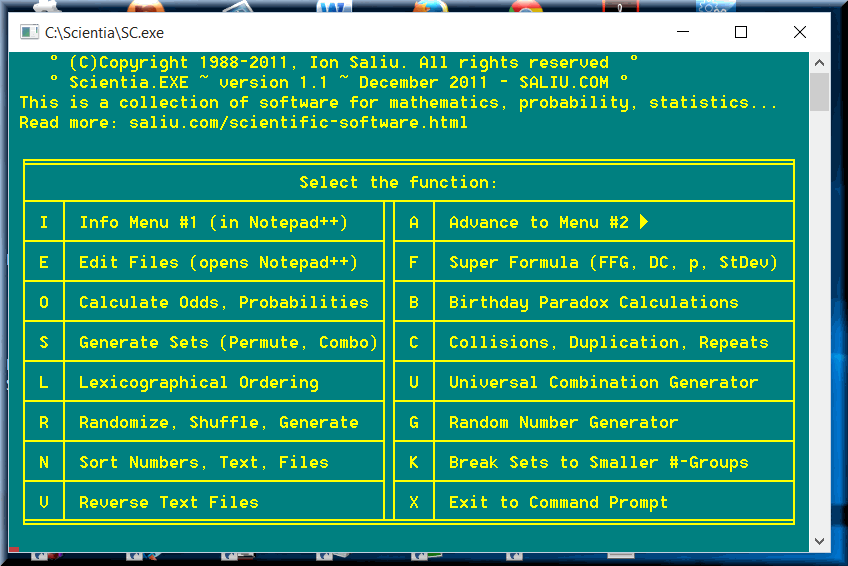
This calculator helps to figure out the odds when playing combinations of various lengths and for various prizes. Many lottery players select 12, or 18, or 20, etc. numbers (picks) and apply so-called lotto wheels or abbreviated lottery systems. It is very easy now to calculate the odds for getting 6 winning numbers when playing a pool of, say, 18 lotto numbers or picks.
A. Sum-up all the numbers between N1 and N2
For example: the sum of all numbers from 1 to 100 is 5050; from 33 to 100 is 4522.
The function calculates instantly the sums of all the numbers from 1 to billions, or from billions to trillions, etc. It is much faster and more convenient than using that hand-held calculator.
B. Sum-up all the numbers in a data file; calculate statistical standard deviation
This function calculates the sum of all the numbers previously saved in a data file in text format; e.g.
17 34 2.5, 100, 99.99, 1000000, 71392.
The file can have one number per line, or multiple numbers per line separated by comma, blank space(s), or combination of both. Do NOT leave any blank lines in the file! The function calculates also:
average; median; minimum and maximum; statistical standard deviation.
The Pennsylvania Cash-5 data file has 2604 drawings (my file). The average is 20.0095. Well, the game draws from 1 to 39 numbers. The theoretical average is (1+39)/2 = 20. My data file in Pennsylvania lottery pick-3 game has 3899 drawings. The average is 4.4817. The game draws 3 digits from 0 to 9. The theoretical average is (0+9)/2 = 4.5. My data file in Pennsylvania lottery pick-4 game has 6056 drawings. The average is 4.4964. The game draws 4 digits from 0 to 9. The theoretical average is (0+9)/2 = 4.5. My Pennsylvania lotto-6 data file has 475 drawings. The average is 34.2589. The game draws from 1 to 69 numbers. The theoretical average is (1+69)/2 = 35.
How about the more complicated game, Powerball? There was a Powerball game with 5 regular numbers from 1 to 49 plus one power ball from 1 to 42. The theoretical average is the weighted average: {(((1+49)/2)*5) + ((1+42)/2)} / 6 = 24.4167. My PowerBall 49/5/42 data file has 514 draws. The average is 24.356. The current Powerball game has 5 regular numbers from 1 to 53 plus one power ball from 1 to 42. The theoretical average is the weighted average: {(((1+53)/2)*5) + ((1+42)/2)} / 6 = 26.0833. My Powerball 53/5/42 data file has 54 draws. The average is 25.605. The actual average is close to the theoretical value even for a small amount of draws!
The standard deviation comes also very close to the calculations of the fundamental formula of gambling. My software takes into account such mathematical requirements. The combinations or sets follow the rules of probability theory and statistics. The combinations are always inside the Gauss bell (normal distribution curve). It's a major factor of optimization.
The numbers have varying frequencies, but the average comes very close to the theoretical value!
See also the interesting case of the 1-2-3-4-5-6 type of combinations: Lotto Combination 1 2 3 4 5 6 Probability, Odds.
C. Calculate N factorial (same as permutations of N)
This function calculates permutations of N or N factorial.
N! = 1 x 2 x 3 x ... x N
For example: permutations of 6 = 720 (1x2x3x4x5x6 = 720).
N must not be larger than 1500—overflow danger!
D. Calculate arrangements of N taken M at a time
This function calculates arrangements of N taken M at a time:
A(N,M) = N x (N-1) x ... x (N - M + 1)
For example: A(10,3) = 10 x 9 x 8 = 720.
Use this function to calculate total trifecta or superfecta combinations in a horse race; e.g. 1,2,3; 4,2,7; 10,6,5, etc.
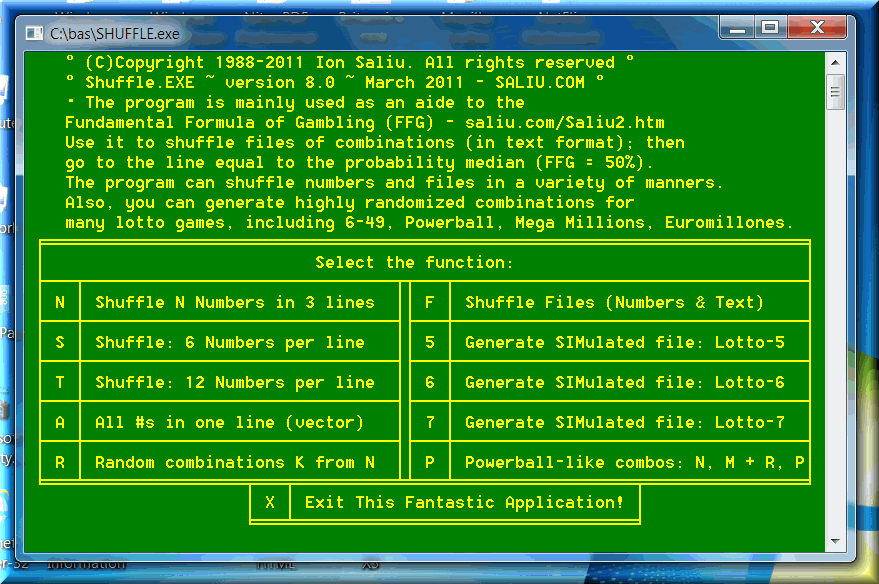
E. Shuffle Pools of Contiguous or Non-contiguous Numbers
Shuffle can shuffle (randomly arrange) a group of contiguous numbers from 1 to N. If the user types 10 at the input prompt, the program will start a continuous process of randomizing 10 unique numbers, from 1 to 10. The sequences look like: 3, 7, 1, 9, 10, 4, 6, 5, 2, 8. The sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 is so rare that it is said only Almighty Number can generate it.
There is another situation: groups of non-contiguous numbers, such as: 1, 44, 33, 55 77 22 66 99 13 111 49 29 25 9 54. Function XII of Super Formula can handle this type of randomizing situations as well. The groups of non-contiguous numbers can be typed at screen prompts. Or, the numbers can be saved to a text file first. The text file can be used as an input device to SuperFormula. The numbers must be separated by space(s), or commas, or combination of both. Also, the numbers can be placed on several lines, or in one column. The user chooses how many times to run the randomization process. The initial group of non-contiguous numbers can be arranged in any order, including sequential.
Shuffle randomizes (randomly arranges) numbers and text or numeric files. The file randomization is one of the most requested features from users of my software. The program applies three methods of randomization:
~ Horizontal: shuffle the order of the items within the line, without changing the order of the lines in the file;
~ Vertical: randomize the order of the lines in the file, without changing the order of the items within the line;
~ Treat the file as a single row/column of data: randomize all the items in the file, regardless of line and column.
The files can have uneven lines; i.e. unequal numbers of items.
The program can also generate combinations for all kinds of lotto games, including Powerball, Mega Millions, Euromillions. The combinations tend to be like in real-life: the software generates unordered random numbers.
 Read Ion Saliu's first book in print: Probability Theory, Live!
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Founded on valuable mathematical discoveries with a wide range of scientific applications, including probability theory applied to scientific, statistical software: Super Formula.

Of interest:

