
Software and Formulae to Calculate Lotto Odds Using Hypergeometric Distribution Probability
By Ion Saliu,
★ Founder of Probability Theory of Life



Written on September 12, 2002 and later.
The page Probability, Odds, Formulae, Algorithm, Software Calculator presents the mathematics and logic of calculating the odds for various games of chance. The odds of lotto games are presented here in more detail.
The lotto games are much more diverse. The diversity widens when the 'power ball' games are taken into account. The lottery commissions set the odds as exactly k of m. Exactly is the operative word here. I thought it was at least. The odds calculated as at least k of m lead to very different values.
The most certain element in calculating the lotto odds is total possible cases. It is known as total number of combinations C(n, k). The combination formula is widely accepted, expert or not.
This is the step that calculates the odds or probability of winning the jackpot: ' 6 of 6', regardless of drawing order. Calculating the odds for other prizes requires a different formula. But we still need the above formula of probability to hit the jackpot. Let's calculate the odds of hitting '5 of 6' in a 6/49 game. We already know the odds of getting '6 of 6'. The 6-number winning combination can be broken in C(6,5) = 6 groups of 5 numbers each. Each 5-number group can be combined with 1 number from the rest of the field: 49 6 = 43. C(43,1) = 43. There is a total of 6 x 43 = 258 combinations. Therefore one winning 6-number combination offers 258 chances of '5 of 6'. Therefore, the probability of hitting '5 of 6' is calculated by dividing total possible combinations C(49,6) by total chances of '5 of 6' (258); 13,983,816 / 258 = 54,200.8 to 1 or '1 in 54,200.8'.
Let's calculate the odds of hitting '4 of 6' in a 6/49 game. We already know the odds of getting '6 of 6'. The 6-number winning combination can be broken in C(6,4) = 15 groups of 4 numbers each. Each 4-number group can be combined with 2 numbers from the rest of the field: 49 6 = 43. C(43,2) = 903. There is a total of 15 x 903 = 13,545 combinations. Therefore one winning 6-number combination offers 13,545 chances of '4 of 6'. Therefore, the probability of hitting '4 of 6' is calculated by dividing total possible combinations C(49,6) by total chances of '4 of 6' (13,545); 13,983,816 / 13,545 = 1,032.4 to 1 or '1 in 1,032.4'.
We can write now a general formula to calculate the odds or probability of various lotto prizes or situations. Hitting '2 of 6' is not a prize; it is just a probability situation.
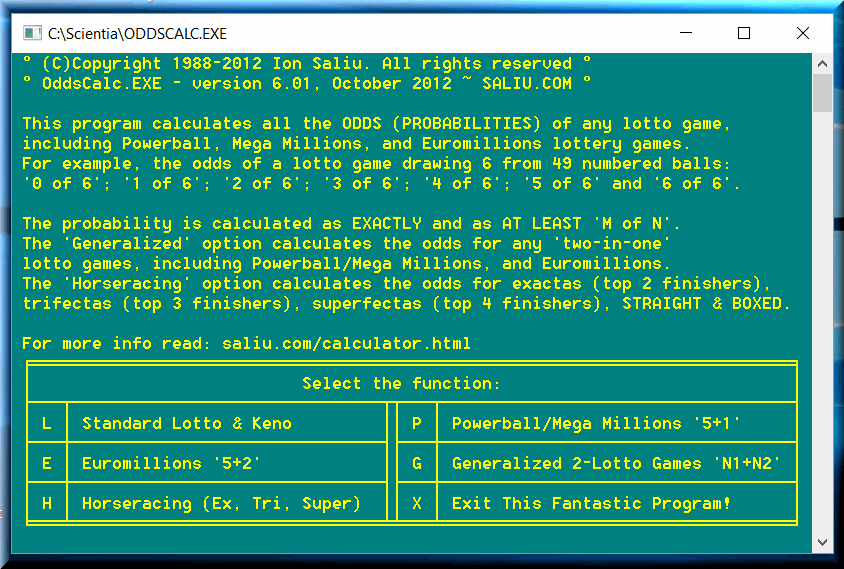
Please be advised that this formula has restrictions. There are impossible situations, such as exactly '1 of 6' in a 6/10 game. The above formula leads to mathematical absurdities in restricted cases. The computer programmer must include code to avoid the mathematically absurd situations. My freeware program OddsCalc does that and a lot more. ODDSCALC calculates the odds of any lotto game, including power ball and keno. If the game draws 6 winning numbers, the program calculates the odds from '0 of 6' to '6 of 6'.
We can use a more complex formula to calculate lotto odds. The formula we used before assumes that if the game draws 6 winning numbers, the player must select 6 numbers and play 6 numbers. But the player has the liberty to select, for example, 10 numbers from the field of 49; then the player must play 6-number combinations from the 10 picks. We can use a more generalized formula to calculate the odds. What is the probability to get '4 of 6 in 10 from 49'? The first formula dealt with 3 elements (numbers): m, k, n; e.g. '6 of 6 from 49'. The hypergeometric distribution probability adds a 4th number; e.g. 'number of picks, s'. The formulation becomes 'm of k in s from n'; e.g. '4 of 6 in 18 picks from a field of 49'. The 'hypergeometric distribution probability' reads:
The hypergeometric distribution probability formula has also restrictions. As before, some cases are impossible; e.g '1 of 6 in 10 from 10'.
My probability software OddsCalc calculates the lotto odds using the hypergeometric distribution probability.
There are many more probability situations that can be calculated using formulas. Many lotto players want to calculate before generating the number of combinations of exactly '3 odd numbers and 3 even numbers'. There are 24 even numbers and 25 odd numbers in a set of 49 elements. The 24 even numbers are grouped 3 at a time. C(24, 3) = 2024 groups. The 25 odd numbers are also grouped 3 at a time. C(25, 3) = 2300 groups. The 3-number groups must be combined so that we get 6-number combinations. Therefore, total number of '3 odd, 3 even' combinations is: 2024 x 2300 = 4,655,200.
How about 2 odd, 4 even? C(25,2) * C(24,4) = 3,187,800.
1 odd, 5 even: C(25,1) * C(24,5) = 1,062,600.
0 odd, 6 even: C(25,0) * C(24,6) = 134,596.
6 odd, 0 even: C(25,6) * C(24,0) = 177,100.
5 odd, 1 even: C(25,5) * C(24,1) = 1,275,120.
4 odd, 2 even: C(25,4) * C(24,2) = 3,491,400.
No other combination of odd/even is possible. If we add-up the combinations of all 7 odd/even groups:
Sum-total: 13,983,816 (of course, C(49,6)).
From another perspective: There are 24 low numbers (1 to 24) and 25 high numbers (25 to 49) in a set of 49 elements. The 24 low numbers are grouped 3 at a time. C(24, 3) = 2024 groups. The 25 high numbers are also grouped 3 at a time. C(25, 3) = 2300 groups. The 3-number groups must be combined so that we get 6-number combinations. Therefore, total number of '3 low, 3 high' combinations is: 2024 x 2300 = 4,655,200.
There are 7 groups of low/high, very similar to the odd/even situation.
The calculations are far more difficult if the two previous conditions act simultaneously. What is the number of lotto combinations of exactly 3 odd, 3 even AND 3 low, 3 high? Let's try to replicate the method in the previous paragraph. We deal now with 4 groups of lotto numbers: 'low-odd', 'low-even', 'high-odd', 'high-even'. We combine the 4 groups 2 at a time in compliance with the restriction: 'low-odd' with 'high-even' and 'low-even' with 'high-odd'. C(12,3) * C(12,3) + C(12,3) * C(13,3) = 48,400 + 62,920 = 111,320.
It doesn't work that way! It is the same situation if trying to calculate, by formulas, the number of lotto combinations for particular sum-totals. As far as I can tell, nobody has ever found such formulae. Only precise lottery software can achieve such tasks. The computer program can generate lottery combinations AND apply various filters. Low/high + odd/even act now as filters; the same in the case of lottery sums.
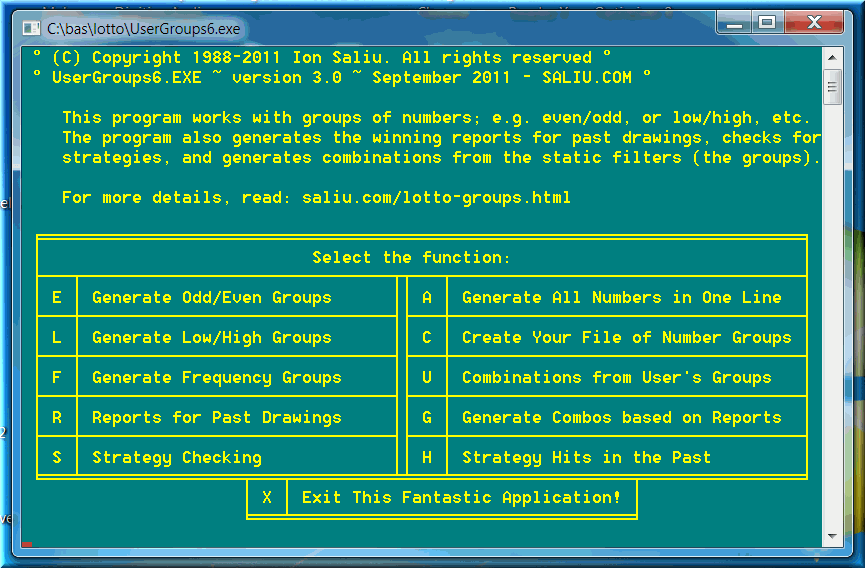
As far as I can tell, nobody has ever written such type of lottery software except for yours truly, that is! My lotto programs are entitled UserGroups6 (for 6-number lotto games) and UserGroups5 (for 5-number lotto games).
Here are some totals for various combinations of low/high and odd/even for a 6-49 lotto game. The lottery software also generates the combinations and saves them to files.
3 odd, 3 even AND 3 low, 3 high: 1,532,168
3 odd, 3 even AND 2 low, 4 high: 1,156,584
3 odd, 3 even AND 4 low, 2 high: 1,059,696
4 odd, 2 even AND 3 low, 3 high: 1,156,584
2 odd, 4 even AND 3 low, 3 high: 1,059,696
4 odd, 2 even AND 4 low, 2 high: 784,278
4 odd, 2 even AND 2 low, 4 high: 881,166
2 odd, 4 even AND 4 low, 2 high: 737,946
2 odd, 4 even AND 2 low, 4 high: 784,278
5 odd, 1 even AND 5 low, 1 high: 86,724
5 odd, 1 even AND 1 low, 5 high: 118,404
1 odd, 5 even AND 5 low, 1 high: 81,576
1 odd, 5 even AND 1 low, 5 high: 81,576
It is very important to remember that the calculations above refer to the condition EXACTLY m of k; e.g. 'exactly 5 of 6'. The lottery commissions only pay one prize of '5 of 6'. Some people expect also prizes for the '4 of 6' groups that a '5 of 6' winning combination is composed of. That's what EXACTLY stands for. If the lottery commissions were to pay for all the prizes that a winning combination is composed of, the odds would have to be calculated as AT LEAST m of k. The odds calculated by the two methods differ to a great extent. The odds of EXACTLY 1 of 6 in a lotto 6/49 game are '1 in 2.4'. The odds of AT LEAST 1 of 6 in a lotto 6/49 game are 6/49 = '1 in 8.16'.
The page Primer: Probability, Odds, Formulae, Algorithm, Software Calculator presents the fundamentals of calculating the odds or probability of various games of chance.
Copyright © MMII, Ion Saliu. All rights reserved worldwide.

Resources in Theory of Probability, Mathematics, Statistics, Combinatorics, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, statistics, combinatorics, plus software.

