Find the Rank, Index or Lexicographical Order of a Lotto Combination in Lottery Drawings (History Files)

• Given a lotto combination, what is its index, or rank, or combination sequence number (CSN), or lexicographic order? We already know the past drawings in a lotto game. What ranks do the lottery drawings represent?

• Proper software (e.g. DrawIndex) should create charts like this one:

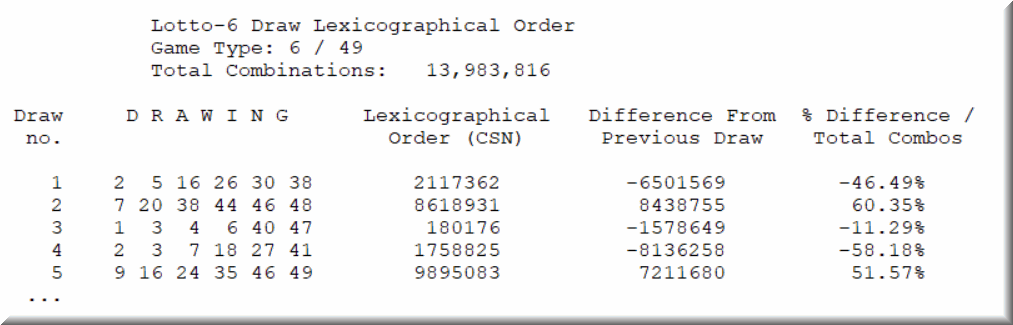
Published on July 07, 2001; later updates.

• There has been a constant interest in this matter, especially in the rec.gambling.lottery newsgroup. The question is: Given a lotto game, can we determine the combination for a particular index? For example, the 49/6 lotto game has a total of 13,983,816 combinations. The first combination (index 1) is 1-2-3-4-5-6. The last combination in the set (index 13983816) is 44-45-46-47-48-49. Nick Kulai Koutras, a lottery researcher with a keen interest in the scientific aspect of the game, posted a link to a computer algorithm. The link is:
netlib.org/toms/
(file 515).

The algorithm was developed by B. P. Buckles and M. Lybanon. It can determine the lotto combination for a particular index in standard lotto games. It cannot be used for Powerball or Euromillions games, without serious reworking. Ion Parpaluck Saliu is the only mathematician and computer programmer to achieve such a task, plus the reverse problem: Find the lexicographical index for a given combination.

The question above represents one half of the sphere. The other hemisphere should answer the following question. “Given a lotto combination, what is its index?” We already know the past drawings in a lotto game. What indexes do the drawings represent? Are most indexes located within the Gauss curve, around the median?

To me, this problem is like a chess problem. Instead of playing a complete chess game, we, sometimes, get a break and solve chess problems. The white moves and check-mates in two. There is some intellectual value to this kind of problems, although the practical value might be questioned.

Perhaps the original B. P. Buckles and M. Lybanon lexicographic algorithm is difficult to understand for most computer users. Plus, it can't answer the second question, without serious reworking. Instead, I use a different algorithm that can be used to answer both questions and be applied to Powerball games as well. My algorithm is quick-and-dirty, but much easier to understand. It can be used with minor modifications to all types of lotto games. The only drawback would be speed of execution. The B. P. Buckles and M. Lybanon algorithm answers the first question instantly. My lexicographic algorithm can take a few seconds, sometimes half a minute for tough games, such as Powerball 5/49/42, or Pennsylvania 69/6. A better than Pentium II PC should run as fast as the original algorithm.

The end result was NthIndex, a program I offer as freeware to registered members of SALIU.COM.

Here is my algorithm for a PowerBall-6 game.

Index# = 0
for A = 1 TO V -4
for B = A+1 TO V -3
for C = B+1 TO V -2
for D = C+1 TO V -1
for E = D+1 TO V
for F = 1 TO K

Index# = Index# + 1
IF Index# = L then 1001

Next F
Next E
Next D
Next C
Next B
Next A

1001 locate 12, 10
….
V represents the biggest of the first 5 powerball numbers. K represents the biggest powerball number. L represents the index for which a user wants to determine the corresponding combination.
If the combination is given and the user wants to determine the corresponding index, only one line is changed. Index# represents a counter. The line IF Index# = L then 1001 is replaced by:
IF A=NUM1 AND B=NUM2 AND C=NUM3 AND D=NUM4 AND E=NUM5 AND F=NUM6 THEN 2004
NUM1 to NUM5 represent the first 5 numbers of the combination the user typed in. NUM6 represents the Power Ball (or Mega Ball). The only requirement is the user type the combination in ascending order. If the drawings in a data file are not sorted in ascending order, SORTING should be run first. But most people can easily sort a drawing!

The algorithm is very fast because it does not use arrays, or disk files.

The program saves the indexes to disk. The indexes are appended to corresponding files. For example, INDEXES.6 for the lotto-6 game. A user can determine the indexes for a large number of past drawings. Then, s/he can load INDEXES.6 in an editor and see what indexes already came out. The index range for past drawings does follow the normal probability rule. I know what most people will do with the results. Instead of selecting 6 or so lotto numbers, they will simply select an index. "Ok. So index 34,245,621 already came out. I think the next index will be 33,398,713. It hasn't come out yet and it's located under the bell ..."

Of course, LotWon is a 'zillion times more versatile and powerful. But a program like NTHINDEX can quench the intellectual thirst of some people. I have known people who don't play chess but love to solve chess problems. Others don't play the lottery, but love to develop or collect lotto wheels. And others don't play combinations but play indexes…

One reason in favor of evolution: We continuously improve and develop. I perfected the lexicographic order analysis to the maximum: LexicographicSets. Also, the software has been greatly improved. Please follow the links below, including the ultimate software in matters lexicographical order. At the time of this writing (the year of grace 2009), my software is absolutely unique; no other lexicographical software comes even close. All four types of mathematical sets are covered. In reverse, the software generates the sets as well (permutations, combinations, arrangements, and exponents): PermuteCombine. There has not been anything quite like it in the world.

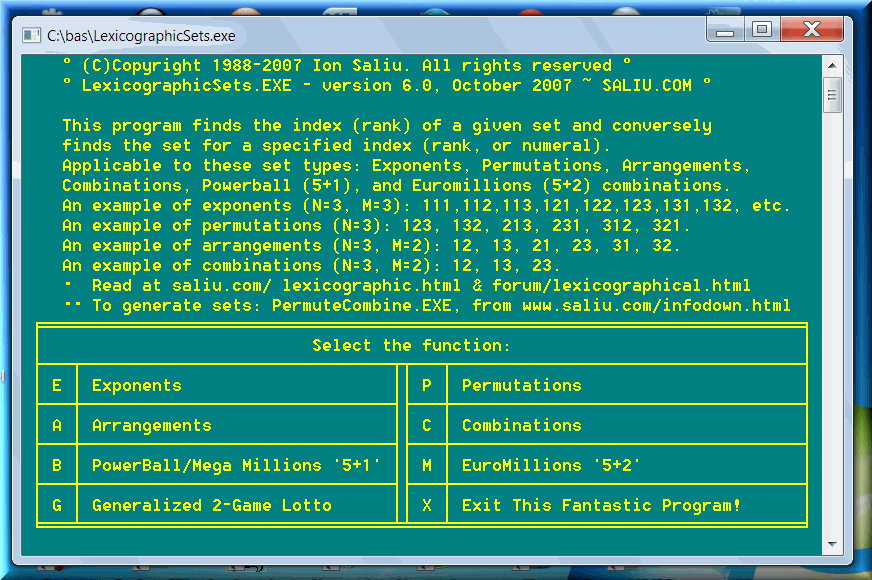
This is a comprehensive list of my writings on the topic of lexicographical order or indexing, including algorithms and software.

• Lexicographic, lexicographical order, index, rank of permutations, exponential sets, combinations.
  This is the most intuitive, if not the best, introduction to the apparently difficult concept of lexicographic ordering (or indexing).

• Lexicographical Order: Lotto, Powerball, Mega Millions, Euromillions.
  This is the most comprehensive and intuitive presentation of the concept of lexicographic ordering (or indexing), including the superior software to tackle the task.

• Combination sequence number or Lexicographic Order Fast Algorithm.
  This is how it all started. I responded to challenges in various newsgroups. I came up with the complementary algorithm to the original algorithm by B.P. Buckles and M. Lybanon" (algorithm "ACM #515"). I offered my lexicographic algorithm bona fide to ACM. A bunch of suckers over there tried to make my algorithm look like their creation, not mine!

• Combination Lexicographic Order, Rank, Index: The Comprehensive and Fast Algorithm.
  I expanded the lexicographical index concept to two-in-one games, particularly the U.S. lotto game of Powerball (applicable to Mega Millions as well); also Euromillions.

• Calculate the combination lexicographic order of lotto data files.
  The introduction of DrawIndex, the software that calculates the lexicographic indexes for every combination (draw) in a lotto results file (see report above).

  The following are older and somehow outdated materials I wrote on lexicographical order subjects. Most of the older software is outdated. Nothing (in the whole world) can beat LexicographicSets or DrawIndex. Sentimentalism is good only to a close extent.
  

• Software combination algorithm formula index ordering.
• Combination sequence number or Lexicographic Order Debates.

Of course, everybody loves to feast on great software, especially when it is free! My combinatorics software (and other categories) is absolutely free to run, for an unlimited period of time. However, only the registered members have a right to download the software. Membership requires a nominal fee — the most reasonable there is to connect to the greatest and most useful software ever created. No kidding! Read the conditions to becoming a registered member: Download Great Free-to-Run Software: Paid Membership Required.

• Download the Software: Science, Mathematics, Statistics, Lexicographic, Combinatorial

  LexicographicSets, the universal permutations, arrangements and combinations lexicographic indexing (ranking);
  DrawIndex - highly automated lexicographical indexing for lotto draw files.
  NthIndex ~ lexicographic indexing superseded by LexicographicSets;
  SEQUENCE ~ lexicographic indexing superseded by LexicographicSets;
  COLORDER - lexicographical indexing for lotto and Powerball only;
  PermuteCombine, the universal permutations, arrangements and combinations generator for any numbers and words;
  Combinations, the universal combinations generator for any lotto, Keno, Powerball game: N numbers taken M at a time, in K steps;
  WRITER, random generator of letters to words, passwords, sentences.