



First capture by the WayBack Machine (web.archive.org) on September 11, 2003.
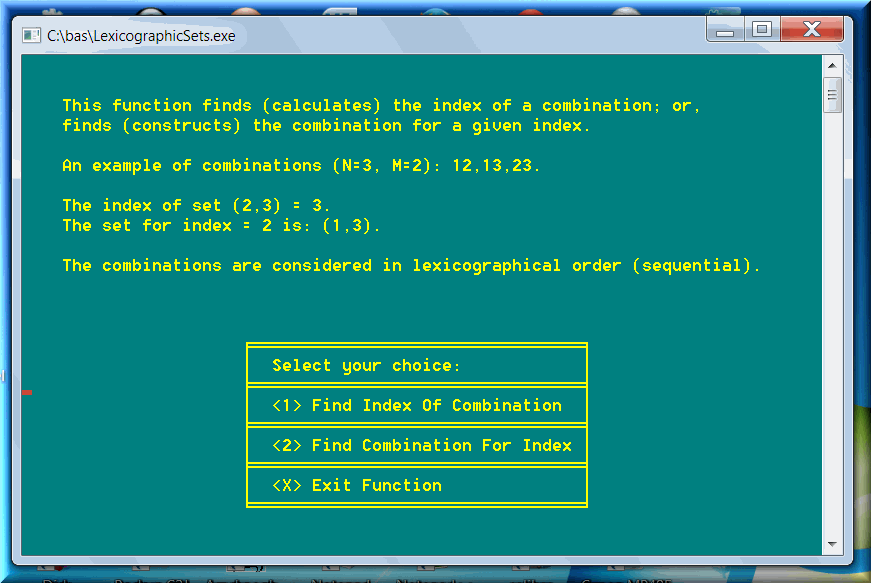
It represents the summit of all lexicographic... make it lexicographical ordering. The program finds (calculates) the index, or order, or rank, or numeral of all types of sets: exponents, permutations, arrangements, and combinations, including Powerball. Conversely, the program finds (constructs) the set for a given index, or order, or rank, or numeral. The sets are considered in sequential, or lexicographic (lexicographical), or dictionary order.
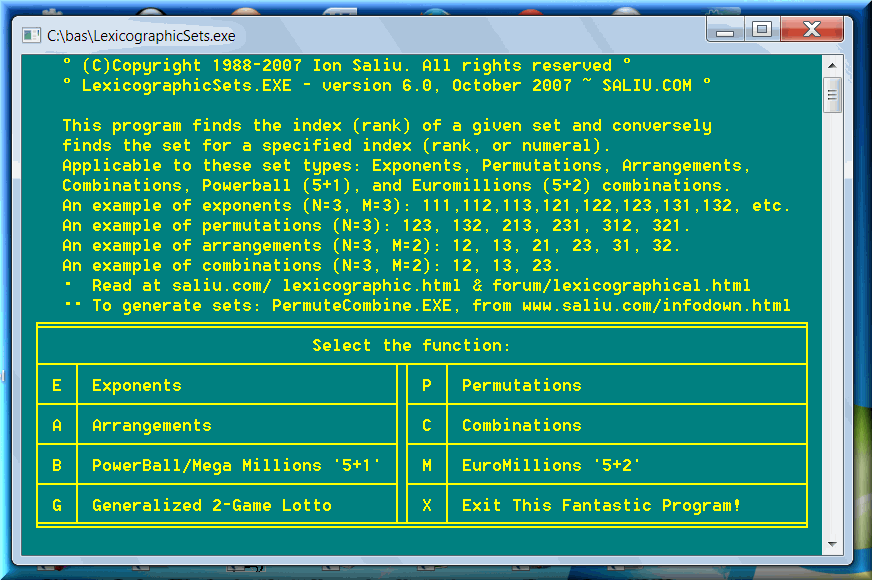
Any finite number of elements can be put together in groups based on certain rules. Such groups are known as sets.
We know very well now how to calculate all possible elements in every type of numerical sets. We can also write software to generate all possible elements in every type of sets: Combinatorics or Mathematics of Exponents, Permutations, Arrangements, Combinations. I am the author of such incredible software: PermuteCombine.exe. It is well-known all over the world, especially for its uniqueness. It is the universal calculator and generator for exponents, permutations, arrangements and combinations. The generation can be set for any numbers or words. As of this time of writing (2009), no other piece of software can do what PermuteCombine can perform.
So, we want to generate all combinations in that lotto game where they draw 6 winning numbers from a field of 49. We can set a program such as Permute Combine to generate all possible combinations in the game (set). If the program is well-written and accurate, it should generate 13,983,816. The generating process will start with this typical combination:
1, 2, 3, 4, 5, 6.
The generating will end with this combination:
44, 45, 46, 47, 48, 49.
We can see that the combinations are generated sequentially, or in lexicographic (lexicographical) order, from the 1st sequence (CSN) to the last.
There are situations when generating all the elements in a set and counting them, and then looking for a particular element is not an efficient process. We can see very easily what the first element in a combination set is, without complex calculations or algorithms.
The combination 1 2 3 4 5 6 comes to mind automatically in the case of a lotto 6–from-49 game (any 6-number lotto game, actually). Also easy: What is the combination of lexicographical order (or index, or rank) 13983816 in a lotto 6–of-49 game? Answer: 44, 45, 46, 47, 48, 49.
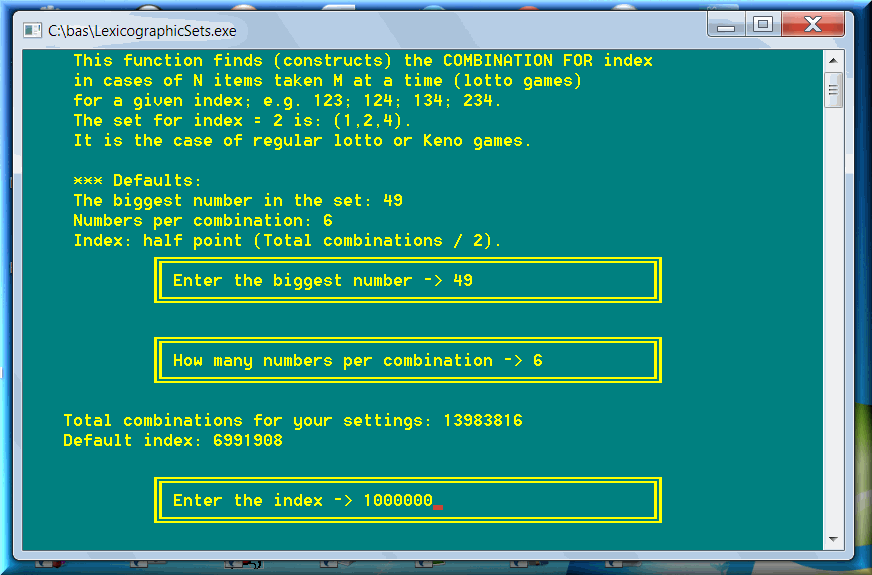
But how about index (or numeral orders) such as 77889, or 1000000, or 6991908? The index #6,991,908 is right in the middle of the set. It is represented by the lotto 6-49 combination 6 7 16 20 28 47.
The calculations are instantaneous with my own program LexicographicSets. The software is founded on some known algorithms, released in the public domain, and mostly on my own algorithms.
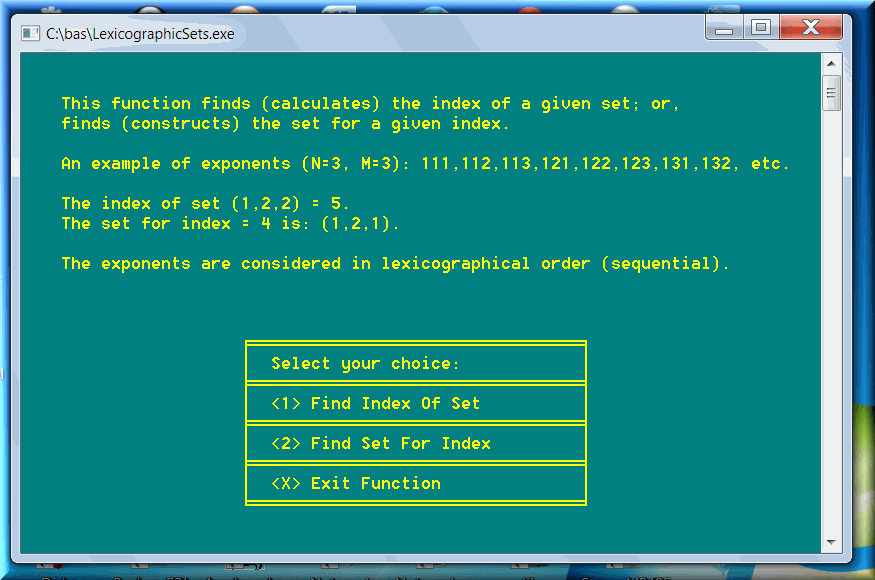
The permutations are also known as factorial, as far as calculation is concerned. Factorial of N or N! = 1 x 2 x 3 x … x N. The factorials grow extremely rapidly.
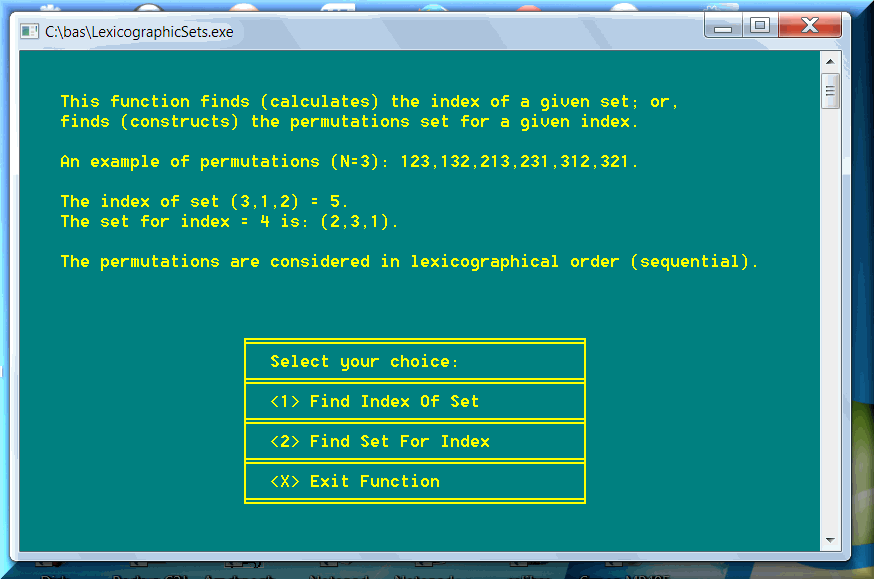
The arrangements of N elements taken M at a time are calculated as N x (N-1) x (N-2) x (N-M+1). The exactas (top two finishers), or trifectas (top three finishers), or superfectas (top four finishers) in horse racing are some of the most common representations of the arrangements.
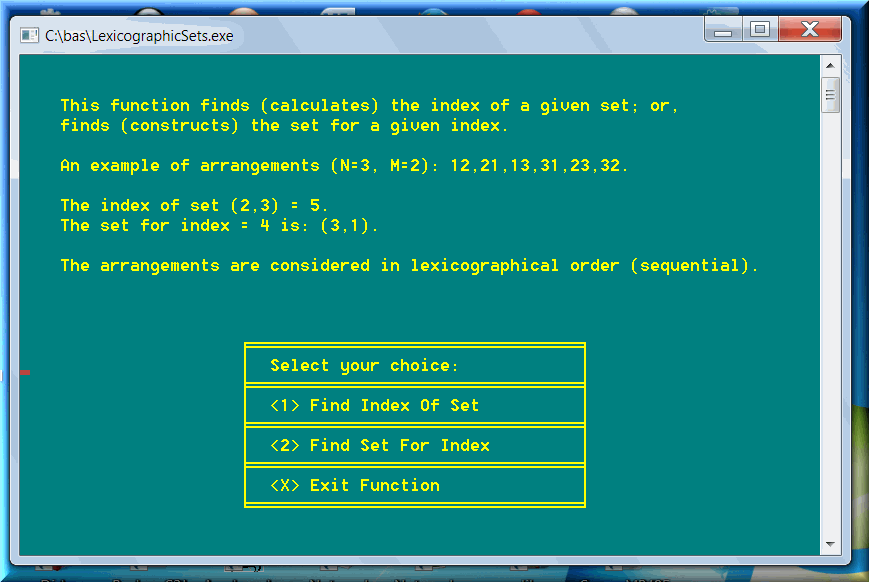
The combination formula is: Combinations (N, M) = Arrangements (N, M) / Permutations (M).
The combinations are the best-known element of the four mathematical entities. The lotto draws are some of the most common representations of the combinations. The software also covers Powerball-type of combinations; i.e. the last number (the 'power ball') can be equal to any of the previous numbers in the combination.
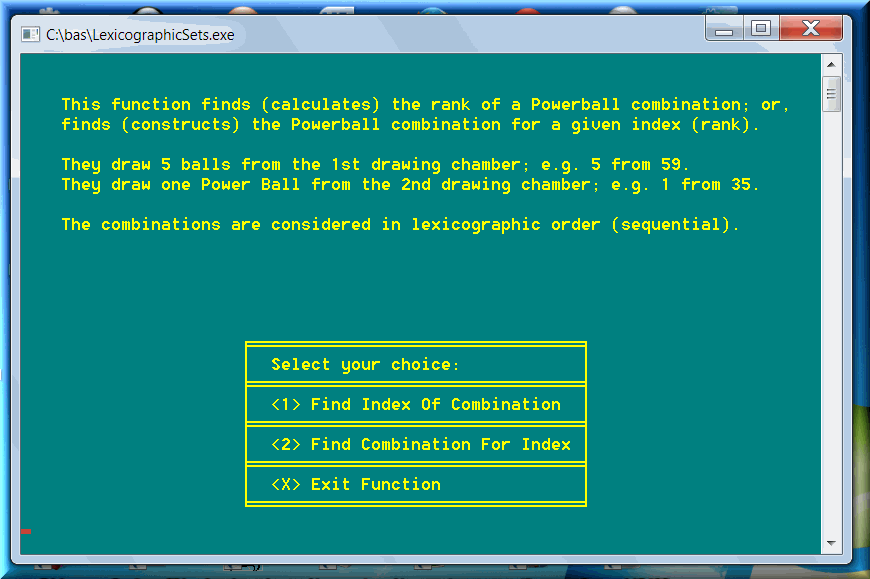
There are special lottery games: Powerball, Mega Millions, Euromillions. They are most accurately defined as two-in-one games. The numbers drawn from the second chamber can be equal to any of the numbers drawn in the first set. The lexicographical order algorithms are based on the one-set lotto games, but there are subtle (and difficult-to-program!) disferrences. Here is a screenshot for the Powerball game (Mega Millions is similar):
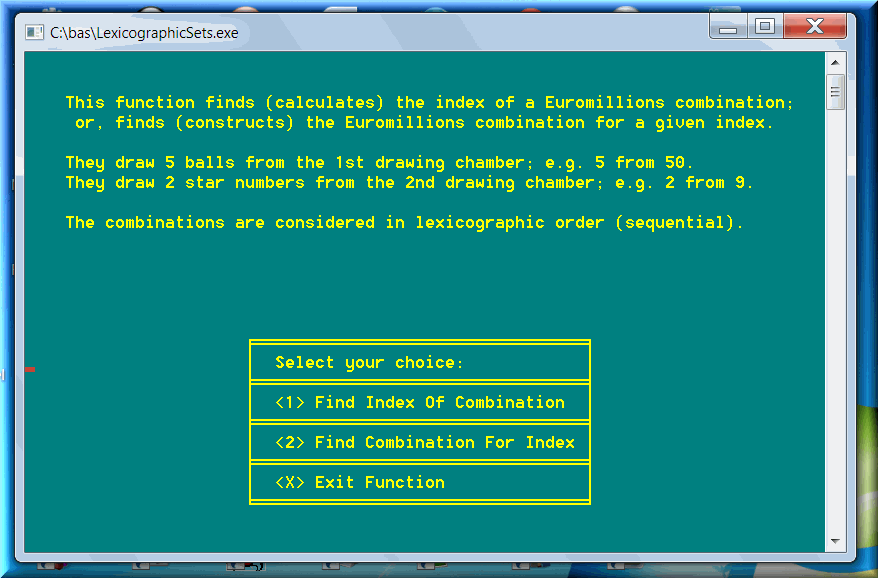
And here is a screenshot for the Euromillions game played in several European countries:
Then, I applied both types of algorithms to all four types of sets: exponents, permutations, arrangements, and combinations. I developed the combinations sets to further dimensions, by creating lexicographic algorithms for two-in-one phenomena (such as Powerball lotto). To this date and my best knowledge, I am the only author of algorithms for lexicographic ordering for all four numeric sets, plus Powerball, Mega Millions, and Euromillions.
This function, present in the modules of all four types of sets, finds the rank (or index) for a given set (e.g. combination):
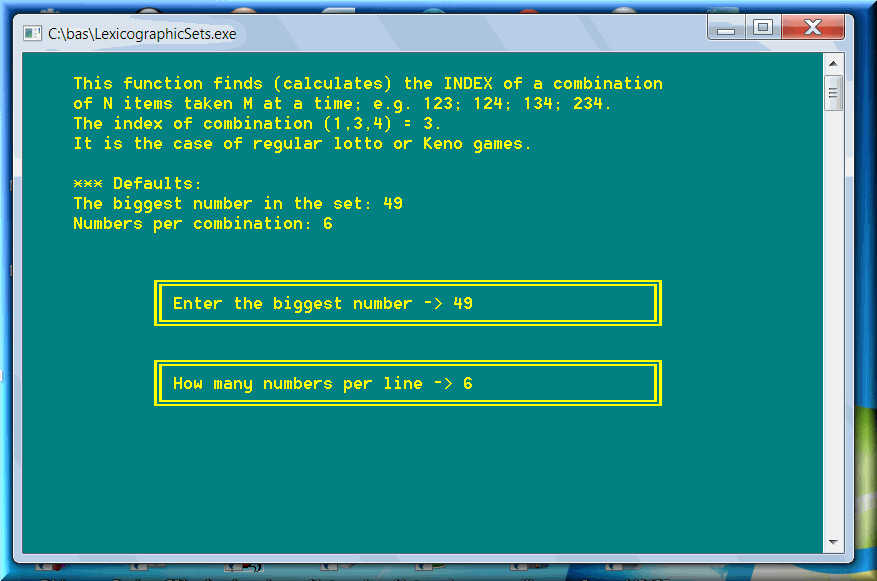
This function reverses the task above and finds the set (e.g. combination) for a given index (or rank) :
Publishing and analyzing the algorithms are tasks beyond the scope of this book. Again, my website is open for business, including in this field. A simple search would lead to many resources at SALIU.COM, including the one-of-a-kind software (nowhere else to be found).
The lexicographical order is very important, however. We notice the case of lotto games, where most combinations appear to be truly random to laypersons. They assess that a combinations like 6-7-16-20-28-47 appears to be truly random. On the other hand, the infamous combination 1-2-3-4-5-6 doesn't appear to be truly random; it appears to be strongly ordered.
In fact, the determining factor is the standard deviation. I call standard deviation the watchdog of randomness. The extremes of the set (the beginning and the end) have combinations with very low standard deviations. Meanwhile, combinations with higher lexicographic orders (ranks, indexes) come from the inside of the set; their standard deviation is closer to the median. The common perception is that the higher the standard deviation the more random a combination is!
Searching on lexicographical, lexicographic, sets, permutations, combinations, etc. etc. yields probably over 100,000 unique search hits! It's a huge mess! Tons of algorithms and source code in every imaginable programming language! I couldn't go too far. I saw newsgroups postings from the early 1980's. It didn't look to me that the issue was ever solved. I mean, I couldn't find the "mother of all sets generating"; or the "mother of all lexicographical indexes"! That finding corroborates with the requests I received to write specific lexicographical indexing and generating software. I was unable to find comprehensive software to tackle sets generating and lexicographic indexing.
I know, the Internet is of gigantic proportions. I assume, however that the two programs I wrote represent the most comprehensive answer to sets generating and lexicographic indexing. The accuracy is also a very important issue. From what I was able to read, there has been a lot of bickering in the newsgroups. It appears that many attempts to tackle the job resulted in faulty algorithms and/or software. I can guarantee that my (comprehensive) software is fault-free to a very high degree. I haven't been able to find a wrong result in quite a few tries.
Speed of execution is also a very important issue. The combinations functions are as fast as it gets. The exponential functions are also close to as fast as it gets. The arrangements functions are slower. The permutations functions are the slowest. I have multiple methods at my disposition. I chose the most accurate ones. Given time, I may come back and insert faster methods. For now, accuracy comes first and second. Speed comes in the third place.
The saying goes that the universities make public the algorithms and source code. Therefore I should make my stuff public, too. Well, the universities are funded. I am not a university and am not funded. Nevertheless, I offer a lot of free software of my own, probably more freeware than most universities.

Resources in Theory of Probability, Mathematics, Combinatorics, Lexicographic Order, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, lexicographical order, combinatorics, plus software.

Home | Search | New Writings | Odds, Generator | Contents | Forums | Sitemap
