
Combinatorics or Combinatorial Mathematics: Exponents, Permutations, Arrangements, Combinations
★ ★ ★ ★ ★
By Ion Saliu, Exponent of Combinatorics




I. Introduction to the Mathematical Sets of Numbers: Exponents (Saliusian Sets), Permutations, Arrangements, Combinations
II. Exponents (Exponential Sets or Saliusian Sets; Ion Saliu Sets)
III. Permutations (Factorial Sets; Exponents without Duplicates)
IV. Arrangements Sets (n Permutations m)
V. Combinations (Boxed Arrangements)
VI. Sets of Letters, Words, Names
VII. Generating Words from Letters, Passwords: Lexicographically and Randomly
VIII. Resources in Theory of Probability, Mathematics, Combinatorics, Permutations, Software
1. Introductory Notes to the Mathematical Sets of Numbers: Exponents (Saliusian Sets), Permutations, Arrangements, Combinations
First captured by the WayBack Machine (web.archive.org) on October 8, 2003.
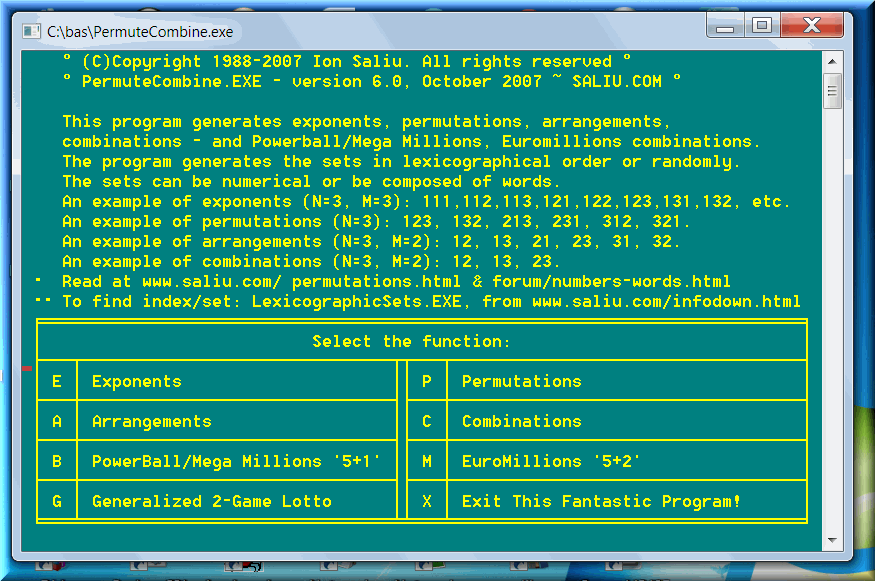
• PermuteCombine ~ Combinatorial software to generate permutations, combinations, arrangements, exponents, factorials for numbers or words in lexicographic order.
PermuteCombine is the summit of all mathematical generation. The program calculates and generates exponents, permutations, arrangements, and combinations for any numbers and words. The sets can be sequential (lexicographic order) or random.
We saw that the probability theory is founded on logic. There is a set of N elements. We can define a sub-set of n favorable elements, where n is less than or equal to N (total possible cases or elements). Probability is defined as the rapport of the favorable cases n over total cases N.
It is obvious by now that probability always deals with discrete elements; i.e. elements we can always count. And thus our main task is to take inventory of all elements in the set and then determine the group of favorable cases. In most cases, such a task is very easy. We can easily count the faces of a die: 6. Next, we only have to state what probability we want to calculate. Let's take the easiest example: The probability to get any point-face (e.g. 5) in one roll of the die. There is exactly one (1) point-face reading 5. Therefore, the probability to get a 5 in one roll of the dice is 1/6, or 1 in 6, or .166666666…
That easy situation of enumeration is quite rare in the grand scheme of things. In many cases, the total number of possible cases can only be calculated by combinatorics, a branch of mathematics.
Any finite number of elements can be put together in groups based on certain rules. Such groups are known as sets. The sets can comprise from 0 elements to infinity (actually, a huge, gigantic, cosmic amount of finite elements). The amount of elements in the set is always an integer number, although the elements themselves can be fractions, decimal numbers, and even transcendental numbers. For example, sale volumes over the past week can read something like {23,457.55, 17,444.02, 8,995.34, 7,234.75, 21,567.99, 9,999.99, 11,234.55}. There are exactly 7 total elements in the set. What is the probability to guesstimate a sale over 10,000? There are 3 favorable cases; p = 3/7.
There is a lot of confusion in the field of sets, both in the academia and among laypersons. The combination and permutation are the most commonly used terms. Worse, people interchange combination and permutation without any restriction! Apparently, in the British system of education, combination and permutation are synonyms! We must establish order and discipline in this classroom! (Don't worry lads! I am mild-mannered!)
There are four distinct types of sets, from the most inclusive to the least inclusive: Exponents, permutations, arrangements, combinations.
The exponents represent the most inclusive of the four types of sets. The exponent set includes permutations; the permutation set includes arrangements; the arrangement set is inclusive of combinations.
The number sets (numerical or numeric) are the most important mathematically. We can substitute the numbers by alphanumerical elements, such as words, names, any strings of characters. In the case of the alphanumerical sets, mathematics works with the indices (indexes) of the respective elements.
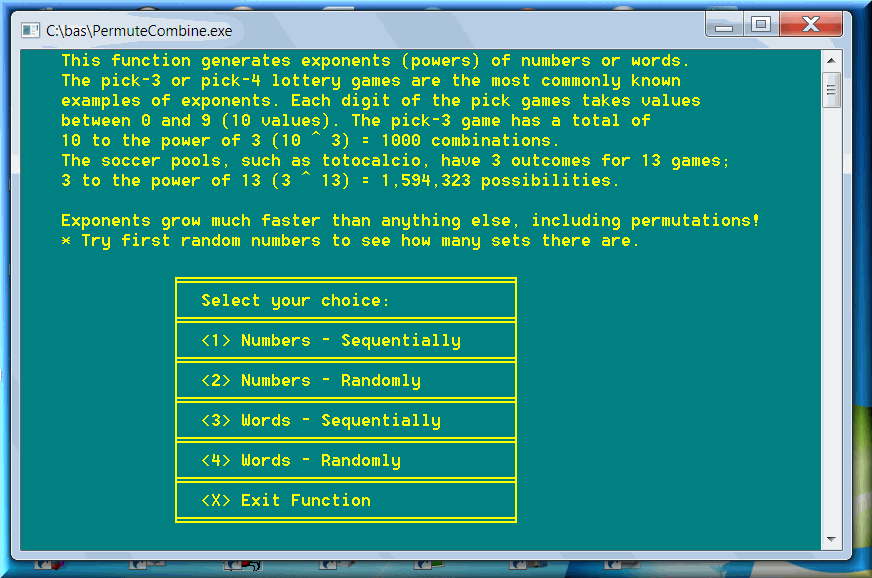
An example of exponents (N=3, M=3): 111,112,113,121,122,123,131,132, etc. (a total of 27 sets). The best-known examples are the drawings of pick or daily lotteries, especially in the United States.
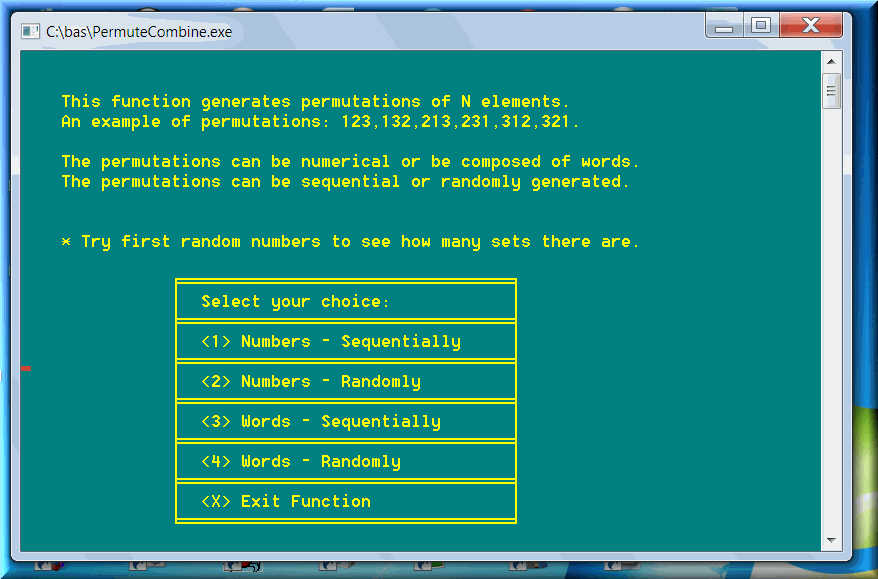
An example of permutations (for N = 3): 1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1 (6 elements: 1* 2 * 3)). There aren't many practical examples for permutations.
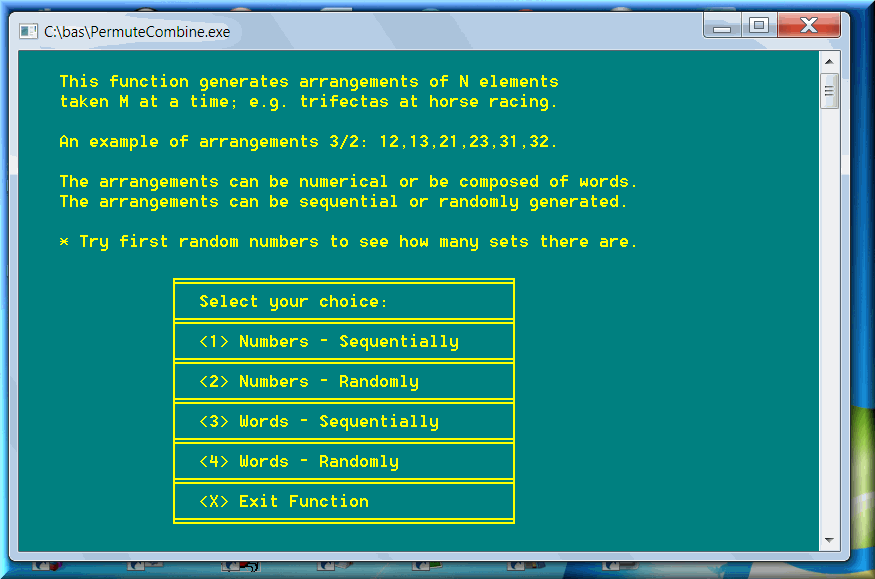
An example of arrangements (for N = 3, M = 2): 1 2, 1 3, 2 1, 2 3, 3 1, 3 2. (6 elements in set: 3 * 2).The best-known examples are the trifectas, the results of horse races (trifectas in the United States, triactors in Canada, top-three-finishers in Britain, etc.)
An example of combinations (for N = 3, M = 2): 1 2, 1 3, 2 3 (3 elements: 3 * 2 / 1 * 2). The best-known examples are the drawings of lotto games, conducted all over the world.
The exponents are very important. They are capable of solving a wide range of probability problems. Since the exponents accept both unique elements and duplicates (repeat-elements), they can solve problems of gigantic proportions and importance. For instance: Can intelligent life, as present on earth, have a duplicate anywhere in the Gigantic Universe? We will tackle the issue later in this book.
The pick-3 or pick-4 lottery games are the most commonly known examples of exponents. Each digit of the pick games takes values between 0 and 9 (10 values). The pick-3 game has a total of 10 to the power of 3 (10 ^ 3) = 1000 combinations. Examples: 013 (equivalent to 0,1,3 or 0-1-3)
The soccer pools, such as totocalcio (in Italy), have 3 outcomes for 13 games; 3 to the power of 13 (3 ^ 13) = 1,594,323 possibilities (total possible cases). Examples: 1,X,2,X,X,2,2,1,1,1,X,1,2 or 1X2XX22111X12.
The parameters for soccer pools (known as totocalcio, pronosport or other names from nation to nation) are: 13 (items per set), 0 (lower bound), 2 (upper bound). 1 represents home victory, 2 is for win for the visitor, and 0 (marked as X on play slips) stands for a tie. The pick-3, pick-4 games have a lower bound of 0, and an upper bound of 9. Items per set: 3 (in pick-3) and 4 (in pick-4).
The formula of exponents is:
Exponent (N, M) = N ^ M = NM
(^ represents the raising to power operator; they also use the superscript as indicator of raising to power or exponent, exponential operator).
The lottery in the State of Pennsylvania has a digit game named Quinto. It draws 5 digits (M = 5), from 0 to 9 (a total of ten elements; N = 10). 105 = 100,000.
The exponents (exponential sets) grow much faster than anything else, including permutations!
The factorials also grow extremely rapidly, but with a lesser intensity compared to the exponents.
The formula of permutations is:
Permutation (N) = N! = 1 x 2 x 3 x … x N
As I said previously, it's hard to find real-life examples of permutations. We can visualize an example by taking all the playing cards in a suit. There are 13 cards, from 2 to A: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A. We can arrange the 13 playing cards in a variety of orders, without removing any card. Factorial of 13 or 13! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 = 6,227,020,800 (more than 6 billion ways!) The first way is 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A; the next sequence is 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, A, K; the 3rd sequence is 2, 3, 4, 5, 6, 7, 8, 9, 10, J, A, Q, K; etc., etc.
n P m = n! / (n - m)!
n! = 1 x 2 x 3 x...x (n-m) x (n - m + 1) x (n – m + 2) x...x n
(n - m)! = 1 x 2 x 3 x...x (n - m)
We can simplify the fraction n! / (n - m)! and obtain:
(n – m + 1) x (n – m + 2) x ... x n
It is the factorial of a series of elements beginning at the term n – m + 1 and ending at the term n. That's the formula of the arrangements:
Arrangements (N, M) = N x (N – 1) x (N – 2) x (N – 3) x ... x (N – M + 1)
The exactas (top two finishers), or trifectas (top three finishers), or superfectas (top four finishers) in horse racing are some of the most common representations of the arrangements. If the famous horse race known as The Kentucky Derby has 20 horses, the total possible amount of straight trifectas is: A (20, 3) = 20 x 19 x 18 = 6840.
The boxed trifectas represent, in fact, the combinations of (N, M). (20 x 19 x 18) / (1 x 2 x 3) = 6840 / 6 = 1140 boxed trifectas. See next.
The combinations are the equivalent of boxed arrangements. We sort the arrangements in sequential (lexicographic) order; therefore, the order of the elements is not important.
The combinations formula is:
Combinations (N, M) = Arrangements (N, M) / Permutations (M) = {N x (N – 1) x (N – 2) x (N – 3) x … x (N – M + 1)} / {1 x 2 x 3 x … x M}
As in this example of the most common lotto game in the world: 6 from 49:
Total possible 6/49 combinations = (49 x 48 x 47 x 46 x 45) / (1 x 2 x 3 x 4 x 5 x 6) = 13,983,816.
The combination set is, by far, the most extensively researched. I reckon it is so because of the lotto games! Even members of the academia want to get rich. No kidding! A group of professors and staff members at Bradford University and College in Britain won the lotto jackpot! It happened on October 21, 2006 in the United Kingdom National Lottery. They played a lotto strategy I started in the early 1990s. I presented that lotto strategy (playing all numbers) and also the corresponding software elsewhere at this website.
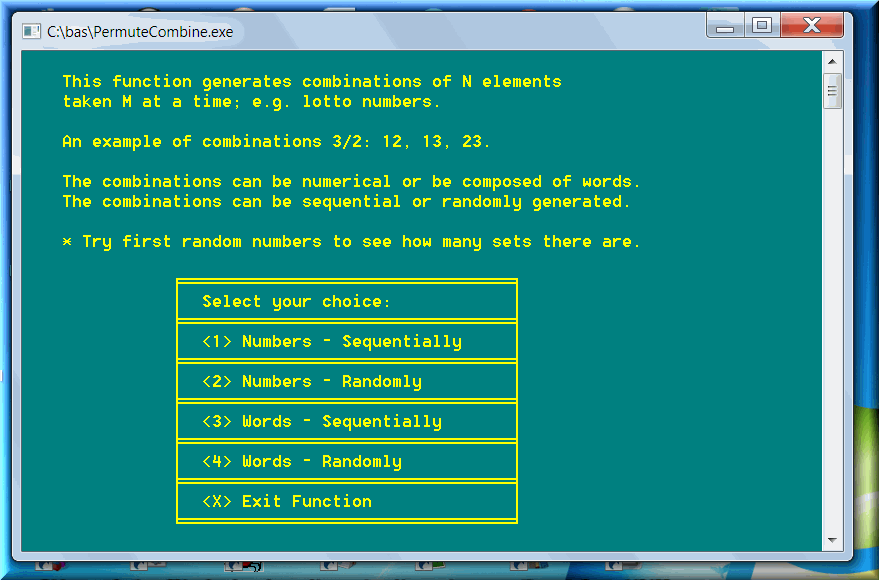
There are special lottery games: Powerball, Mega Millions, Euromillions. They are most accurately defined as two-in-one games. The numbers drawn from the second chamber can be equal to any of the numbers drawn in the first set. Here is a screenshot for the Powerball / Mega Millions game:

And here is a screenshot for the Euromillions game played in several European countries:
Permutations
permutation, sequential
random
lexicographic
Lexicographical, Order,
combination
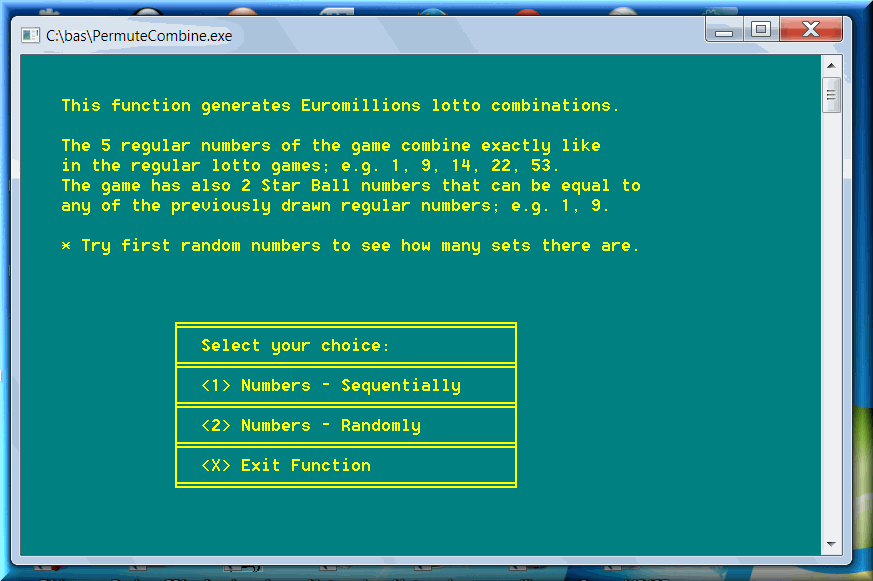
Here are fragments of the output file for the word-generating option for Combinations in Permute Combine:
- Combinations, Lexicographic Order (N = 6, M = 5, 6 elements total)
Permutations | permutation, sequential | random | lexicographic | Lexicographical, Order, |
Permutations | permutation, sequential | random | lexicographic | combination |
to...
permutation, sequential | random | lexicographic | Lexicographical, Order, | combination |
The word generation can be used at horse races to generate sets of horse names, instead of post position numbers. This feature is useful in sports betting, too. A user can write, for example, all the NFL teams in a list file. Then generate parlays every week, using the feature: Arrangements: Words, Random. Select, for example, 5 words (teams) per set. Check the output and disregard the sets with teams from the same game for that week.
The permutation, exponential, and combination word features can work as well. No word generation for Powerball, Mega Millions, Euromillions — not of much use, in my mind.
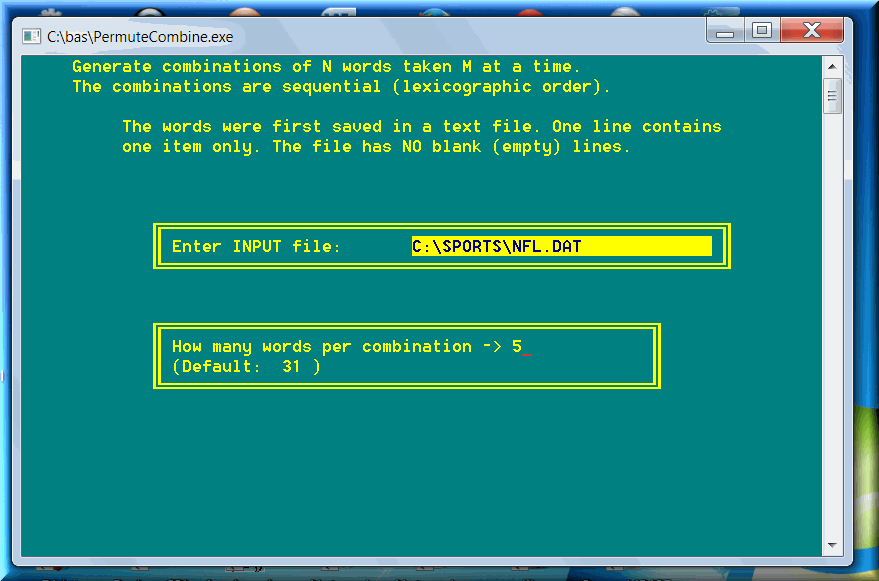
Suppose we write the 26 letters of the English alphabet in a 26-line text file, one letter per line. We can generate an astronomical number of permutations (words). But the permutations have a fixed length (number of letters), whereas the natural languages have words of a variety of lengths. The exponents serve the purpose better. The words vary from one letter to some teens. The first letter of a word can be from A to Z; the second letter of a word can be from A to Z; the third letter of a word can be from A to Z; etc. The words can have repeat letters.
I wrote another computer program that generates random words in a manner close to the natural languages. The words can have repeat letters; the words are of variable length; a word must contain at least one vowel. The combinatorics software is named Writer.


Home | Search | New Writings | Fundamental Formula | Odds, Generator | Contents | Forums | Sitemap
