


I. Fundamental Mathematical Confusion: Probability and Degree of Certainty
II. Events Cannot Repeat Ad Infinitum During a Lifetime
III. Probability Is Free from Mechanics
IV. Is History Any Indication? You Bet!
V. How About Them Streaks? Probability Theory Is the Mathematics of Streaks
VI. Resources in Probability Theory, Mathematics, Statistics, Combinatorics
That is the innocent part, axiomatic one. There is a minor but very vocal group of humans who create the confusion intentionally. Their intention is hate-based and serves selfish purposes. I can tell you first-hand that some react intensely hostile because they want me to remove such writings from my website; and, then, they could take my ideas and get credit for them! The casinos also have a big problem with my theories because they show the reality. Such mathematical truth can lead to superior play from many gamblers. The casinos do not want people to realize the distinction between probability and degree of certainty.
This is issue has caused the most trouble for me in public places, such as newsgroups or forums. I trigger intense hostility towards yours truly as soon as I make the distinction between the three elements. The probability p is an abstract concept. It is the constant of a particular phenomenon. It has no life of its own. If you conduct one trial for an event of probability p then the degree of certainty DC is equal to p.
It is the only case when DC = p. That is the main reason of the fundamental confusion that started this essay. If we toss a coin one time, the degree of certainty to get heads is 0.5, which is also the probability of tossing heads. But the degree of certainty is equal to 0.75 to get heads in two consecutive tosses. So, if the first toss was tails, I expect heads with a degree of certainty of 75%.
That's when the roar of hatred reaches a peak! Many mouth-foamingly shout that the expectation is still 50% before the second toss! They only see the constant probability p, but are blind to the other two elements: Number of trials and degree of certainty!
"1) The probability against your winning the lottery is non-zero.
2) Therefore the event against your winning the lottery will repeat ad infinitum.
3) If you bet on heads in coin-tossing, then the tails will repeat an infinite number of times."
One can write books against the "points" above. I can afford to only touch those "points". All humans of Reason will easily comprehend and validate my ... points.
• Everything in the Universe has a non-zero probability, except for absurdities. Absurdity is not to be confused with impossibility. Mathematics defines impossibility as an event of a probability infinitesimally close to zero. Absurdity is a phenomenon without a valid mathematical relation (formula, equation, etc.)
One common caveat is absolute certainty. Most humans believe that certain events are…certain, while other phenomena are random. A human considers his/her tomorrow as certainty. The same human considers his/her 5/39 lotto game to be random. Well, it isn't just like that, axiomaticule!
I will make usage here of very conservative statistics regarding unexpected loss of life in the U.S. of A. It is a very conservative stat that at least 50,000 Americans die, UNEXPECTEDLY, THEREFORE RANDOMLY, of gunshots — every year. At least 50,000 Americans die, UNEXPECTEDLY, THEREFORE RANDOMLY, in traffic accidents — every year. At least 150,000 Americans die, UNEXPECTEDLY, THEREFORE RANDOMLY, because of taking prescription drugs — every year. Now, that amounts to 250,000 Americans who had been certain of their tomorrows. Unfortunately, they died with the wrong perception of randomness and certainty.
Let's take the above stats to a daily basis. 250,000 / 365 = 685 Americans who die unexpectedly every day. We can calculate here a parameter named 'randomness of ungodly death' by the notable statistician Bern Abio in the XVIII century. There are around 300,000,000 (three hundred million strong) Americans (we can include the Canadians here as well, for they are virtually the same breed of free men and women who are guaranteed the freedom of reasoning).
685 / 300000000 = 0.00000228333… or '1 in 437956' the (favorable?) odds of dying unexpectedly (randomly) in America. Wow! It's kind of scary! It's somehow easier to win the 5/39 lotto jackpot than to survive to your next day, if you live in America! Unfortunately, the situation is even worse, much worse, in most places of this great world of ours!
By the way, the odds of winning the 5/37 lotto jackpot is '1 in 435897'. So, the odds are about the same that you will die tomorrow without notice — compared to winning the 5/37 lotto jackpot with one ticket in one try.
Does it imply that the humans should not take any reasonable action because the probability of their dying randomly is non–zero? Of course not! The reasonable humans take a multitude of actions with the expectation to improve their odds of surviving each and every day.
The probability of the Moon colliding with the Earth is greater than zero. In fact, the Moon was born as a result of a collision of the planet Earth with a planet the size of Mars. Now, shouldn't reasonable humans take any action in order to survive? Should they just cover their heads in ashes and wait for the collision of the Moon with the planet Terra? Of course not!
The theory of probability is based on a fundamental formula. The probability p is defined as the rapport of favorable cases, n, over total possible cases, N:
That parameter p is a constant for its respective phenomenon. For example, p is always ½ (or 0.5) in coin tossing; 1/6 (or 0.16666667) in getting one particular face of a die; 1/1000 (or 0.001) in hitting one particular pick-3 lottery number (e.g. 013). The parameter p remains the same in every calculation we do in probability theory. If I take 10 coin tosses, I always set p = 0.5 in toss #1, toss #2, toss #3,…, toss #10. I know that the probability to get heads is 1 in 2 in the 1st toss, 1 in 2 in the 2nd toss, 1 in 2 in the 3rd toss,…, 1 in 2 in the 10th toss. Yet, the probability to get 10 heads in 10 consecutive trials is 0.5 ^ 10 = 0.000976. You do the experiment. You'll definitely notice that 10 consecutive heads occur about once in 1000 experiments (ONE experiment here is tossing the coin 10 times).
You take the pick-3 lottery game. There are 1000 possible outcomes, from 000 to 999. The individual probability p is 1/1000 (or 0.001). The probability to win with the pick–3 combination 013 is 0.001. Let's suppose that 013 hit today. What is the probability that 013 will hit again the very next drawing? There is a subtle distinction here.
You can run my probability software Collisions.EXE. The extraordinarily powerful program can perform huge number calculations with amazing ease.
This pick-3 example represents a case of probability of coincidences or probability of collisions. The most famous case in this category is represented by the Birthday paradox. Invite, randomly, 23 persons to a common place, a room, for example, or a desert tent. You can pick 23 camels, for that matter; the only requirement is to know precisely the birthdays of every camel. The birthday paradox tells you that the probability is 50-50 that at least two camels (or horses, or jackasses) share the same birthday, if 23 individuals are concerned. Many people are victims of confusion here. They confuse the probability of the birthday paradox with the probability of guessing the birthdays of two camels. I made the same confusion in the past. I don't think I was smoking cigarettes at that time, Camels or other cigarette brands. Who knows what Osama is smoking that makes him so mad…probably he smokes pulverized human bones...
Okay, the probability of a pick 3 repeat is 0.100000000000000002%. That's about a li…………ttle better than 0.001. So, if a pick–3 combination hit today, it has virtually the same chance to hit the very next drawing.
COLLISIONS.EXE is extremely precise and picky about it! We must make certain that the following point is understood. The probability above refers to ANY of the 1000 pick–3 combinations. We do not nominate ONE particular pick 3 combination to repeat the very next draw.
If 10,000 lotto 6/49 drawings are conducted, the probability is 97.2% that at least two combinations will be the same (duplicates). If 5,000 lotto 6/49 drawings are conducted, the probability is 59.1% that at least two combinations are the same. If 1,000 lotto 6/49 drawings are conducted, the probability is 3.5% that at least two combinations are the same. If 100 lotto 6/49 drawings are conducted, the probability is 0.0035% that at least two combinations are the same! You can see, it takes a large number of events to have a lotto 6/49 repeat–combination. How far is that from a combination repeating in each and every lotto drawing?
When we refer that PRECISELY one particular combination will repeat, the probability is faaaaaaaaa…ar lower. If we take, for example, the pick3 number 013 to repeat in the next draw, then the probability may show '1 in one million'. That was the subtle difference I was talking about a while ago.
There is so much more to it! Yes, the probability of repeating ANY outcome the next drawing is virtually the same compared to coming out just before that. Delving deeper always harvests more pearls. I analyzed — thoroughly, I believe — real-life roulette spins recorded at the Hamburg, Germany casino (Hamburg Spielbank). The software (my own creation, possibly my computer program #500–something) shows that the roulette numbers do not… like to be followed by themselves! Like it or not, Spiel, 25% of the roulette numbers repeat more than 55% of the time after a particular roulette number. That is, any particular roulette number always prefers other numbers to pair with — other than itself. Well, I know why, and you can, too. It's all about FFG.
Again, another big book can be filled around this topic. Suffice to say for now that the numbers are followed by different numbers significantly more often than being followed by themselves. The length of data I analyzed is statistically significant: About 10,000 spins. That's more than 250 times total possible outcomes in the double-zero roulette. And that is REAL life data. Can you think of over 250 times total outcomes in a lotto game? If you do, Psychosama, you ain't got knowledge of length of life. You better think of your tomorrow...
It is the same thing when considering the probability of a pick 3 lotto combination to match its date expressed as a 3-digit number. Again, my freeware comes to the rescue: DatePick3.EXE. The extraordinarily tiny program can perform huge number calculations with outlandishly amazing ease. It calculates the probability for the ANY cases. If we consider ANY of the pick 3 combination matching its corresponding 3–digit date format, then the probability is 1 in 1337. If you check all pick-3 drawings in the world, you'll find that the results are very close to 1/1337.
Now, if you take one particular pick–3 combination, e.g. 111 to hit on January 11 expressed as 1/11 or 11/1 and check all the drawings in history, the probability will show 1/365000. I know, there are not enough real–life drawings to accommodate precise calculations. Still, DatePick3.EXE will serve you excellent simulations.
Oh, no, pahleese! Don't take the 911 on September 11 (9/11) 2002 in New York lottery example. It was a farce founded on humane reasons. I still believe that the New York lottery officials must come forward with the TRUTH. What they did was understandable. I have no problem with that. I only have a serious problem with hiding the truth. It would be highly entertaining to read all the discussion, behind closed doors… I'm sure that the governor and the mayor were involved, and they pushed the green light buttons…
The answer is YES. The probability formulas don't give a damn about the mechanics. The p, and n, and N, and DC are abstracts. They are numbers. The probability to get Heads is always 1/2 or 0.5. The p doesn't care what coin was tossed. The denomination or the nationality of the coin doesn't matter at all. The only requirement is that the coin is unbiased. In fact, the probability would love to have a new coin every time, for every toss. Thus, the unbiased requirement is satisfied. A coin will get biased after a number of tosses. Yes, the material, the metal is important when splitting the hair – a huge number of trials make a huge difference!)
One more important requirement is the SERIAL factor. The experiments (trials, coin tosses, etc.) must be serial. They come ONE AFTER ANOTHER. The probability formulae take into account one serial event at a time. The opposite is parallel events. For example, two coins are tossed at the same time. The events are parallel. The only way we can research them is to record every coin separately. You conduct an absurdity if you record the spins of several roulette wheels as a single phenomenon.
There is a situation that triggers plenty of questions. I get emails regarding the two daily drawings in the pick 3, 4 lotteries. For example, the Pennsylvania lottery conducts a mid–day drawing and an evening drawing in the pick-3 and pick 4 lotteries games. Thus, the drawings are serial, not parallel. One can consider the pick 3 game as one game. Record the mid-day drawings and the evening drawing in the same database. At the same time, I am right if I keep separate records, and thus view the drawings as two different games.
In fact, every lottery game is a multiple game. They draw several times, before the official drawings. The pre–official drawings and the official drawing represent a serial phenomenon. But I would not record all the fake drawings in my database. The only thing that the multiple draws influence is the timing of a strategy. With or without multiple drawings, no phenomenon can escape the Fundamental Formula of Gambling.
By the way, I used to record the mid–day drawings and the evening drawings in the same database. But I gave up. I only record the evening drawings in the pick–3 and pick–4 games. It's about a working schedule. I work the first shift, therefore I am unable to play the mid–day games. If one works the second shift, then I recommend playing the mid–day game, not the evening edition.
Like I sez, big books can be filled on these topics. Randomness and Certainty are fighting brutal wars every split of a second, of every second, and minute, and hour, and day, and week, and terrestrial year, and century, and millennium, and era, and galactic era, and universal era ... ad infinitum. Each and every one of us might die tomorrow — absolutely unexpectedly and randomly. But should we give up all of our strategies and systems of living because the unfavorable odds are non-zero? NOT!
Yet, filling big books with all kinds of formulas and strategies can have consequences. I was directed to a forum in Romania. There was a post by a Romanian journalist who had contacted me regarding my activity. The journalist had also interviewed another Romanian, a casino executive. That executive of the association of the casinos in Romania was sent to study at a curious "education" facility. It is the so–called University of Gambling in Nevada!
The executive told the reporter that he had knowledge of two Romanian Americans who are on the blacklist of every casino in the United States. The first Romanian American is a most dangerous player regarding cheating in the casino. It's not me, by the dog in Egypt I swear. I am the second Romanian American on the blacklist of every casino in the USA. I am blacklisted because I am supposed to possess every winning formula for every type of gambling! I swear by the dog in Egypt, I bear it as a badge of honor my being blacklisted for the sole motive of my knowledge by all the casinos in the great land of the US of A!
"A fresh start ain't fair," concluded Blaise Pascal in his impeccable French. The player in the lead had already an advantage that he had earned. Pascal was new to the field of mathematics known as theory of probability. As a matter of fact, Pascal was inventing probability theory! So, his calculations looked rather complicated — nonetheless convincing. The past counts.
Today we possess many more tools, including a more advanced science, plus we have computers and software. We will use here my free program SuperFormula.EXE to perform probability calculations, no matter how complicated. The de Méré problem can be solved by the probability of the binomial distribution. It is also known as he probability of M successes in N trials.
We must suppose that the two players are equally skilled, thus the winning probability is 1/2 or 0.5. The first player to win 2 games wins the match. The trailing player must win the next 2 of 2 games. The binomial distribution probability for 2 successes in 2 trials is 0.25 or 1 in 4. The player with the lead needs to win only one of 2 games. The binomial distribution probability for at least 1 success in 2 trials is 0.75 or 3 in 4. Clearly, the player in the lead has a better chance to win the match after its resumption.
What if the bet were the best of five? Again, the match resumes after one player leads 1–0. The first player to win 3 games wins the match. The trailing player must win the next 3 of 4 games. The binomial distribution probability for at least 3 successes in 4 trials is 0.31 or 1 in 3. The player with the lead needs to win only 2 of 4 games. The binomial distribution probability for at least 2 successes in 4 trials is 0.69 or 1 in 1.5. Clearly, the player in the lead has a better chance to win the match after its continuation.
• • The American professional sports are founded on the playoff concept. The best of seven is the predominant format. The team with the first four wins advances or, ultimately, wins the championship. Let's analyze three situations.
~ after 2 - 0
~ after 3 - 0
Of course, a professional game is not exactly a coin toss. The teams are pretty well matched, nevertheless. They call it parity.
It was believed to be impossible to come back from a 3–0 deficit and win a series. It happened only four times in North American professional sports.
It happened three times in professional hockey (NHL): 1942 (Toronto Maple Leafs), 1975 (New York Islanders), and in 2010. The latest was accomplished by the Philadelphia Flyers against Boston Bruins on May 14, 2010. There is more amazing attached to that hockey game. The Flyers were trailing 3-0 in the series. Also, in game 7, the Flyers were trailing 3-0, but they came back and won Game 7 by the score of 4-3. The series was also 4-3 in favor of the Flyers.
The other come-from-a-0-3-deficit event happened in Major Leagues baseball. The Boston Red Sox defeated the New York Yankees in 7 games, after trailing 3 games to none. The Red Sox went on to win the pro baseball championship (the World Series) in 2004. If the games were played on neutral sites, the statistical data would be even closer to the theoretical probabilities.
• • • One easy method is to apply the Saliusian sets (Ion Saliu sets). The number of elements in the set is calculated by exponentiation (raise-to-power mathematical operation).
There are problems like this one. Suppose you are told that two visitors will show up at your place. Each visitor can be male (M) or female (F). You are told that one of the visitors is female. What is the probability that the second visitor is also female?
There are 4 possible cases (2 to the power of 2):
FF
FM
MF
MM
However, one case is invalid: MM. We already know that one of the visitors is F. In only one of the three cases both visitors are females: FF. Thus, the probability that the other visitor is also female is 1 in 3 (0.33). The probability is 2 in 3 (0.67) that a female is accompanied by a male visitor.
This problem can have a twist, however. You are told that precisely the visitor to the left is female. What is the probability that the visitor on the right hand side is also a female? The only valid cases now are FF and FM. The probability that the visitor to the right is also female is 1 in 2 (0.5).
To see more clearly the role of the past, we can toss two coins. We know that one of the tosses was heads. What is the probability that the other coin showed heads also? Same as above.
I have been aware of the role of history in probability for a long time. The events can repeat — and they will repeat. Also importantly, the events will miss — and they will miss or skip. The skips play an essential role in my theory, systems, and software.
We can deduce a third important element in probability: Streak. “It's all about the streak!” some gamblers say. “I am on a hot streak”. A baseball hitter is said to be in a slump when he goes through a long losing streak (not hitting the baseball).
The casinos, especially online gambling sites, want players believe that losing 10 hands in a row, or 20, or even 100 hands in a row is a natural fact of life! But guess who's losing? Yup! Only the player! Don't ask why the house doesn't lose 20 or 100 hands in row! You might get ugly phone calls from unknown numbers, like I do now and then!
We usually divide the streaks in two categories: winning streaks and losing streaks. In reality, they represent one and the same concept. An event occurs, or happens, or appears, or hits in a number of consecutive wins. We call them streaks. The streaks have a length; i.e. number of consecutive hits. The length can be from 1 to N. We put Infinity aside, for it won't happen in a lifetime. In truth, Infinity doesn't occur at any given moment: TheEverything is finite at any sharp moment in Time.
I toss a coin. I am interested in heads (H), for example. I can record one heads followed by tails (T). The streak is one, in this case. I can record also one tails, then 2 heads followed by tails; the streak is two, in this case. We can symbolize the case as THHT. A THHHHHT case represents a five-streak (winning streak for Heads).
Do the streaks occur equally, regardless of length? Of course not! Only the above gambling entities want gamblers to believe that. Mathematics doesn't agree, however. The shorter the streak, the more often it occurs in a given number of trials.
You can easily verify by tossing the coin and recording the results. If you do it 1000 times or so, you will notice that the streak_1 occurred about the same number of times as the other streaks combined. You will also notice that the 2-streak is twice more frequent than the 3-streak… and so on. The same is true for tails since it has a probability equal to the probability of heads: 1 in 2 (or 1/2, or .5). The ratio between various lengths of streaks is determined by the probability of the event.
I already wrote the software for you. It calculates very easily how many streaks of a particular length you can expect in any given number of trials. The name of that grandiose program of mine is Streaks.EXE. Download it from my software download site (see the link in the footer of this page). The probability program belongs in the software category 5.6 (scientific software).
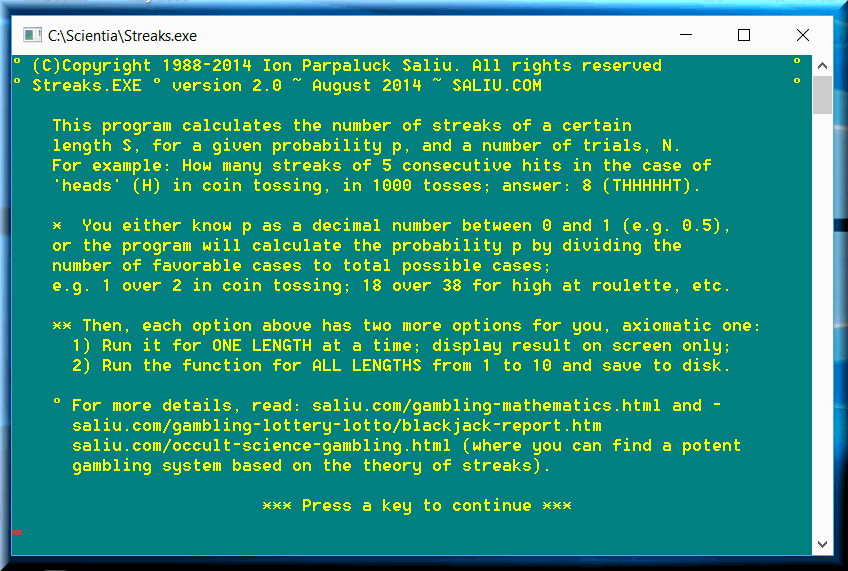
How many streaks 8 heads in a row? There is 1 (one) such a streak in 1000 tosses. The same is true considering 9 heads in a row in 1000 tosses. But the program calculates 0 streaks of 10 consecutive heads in 1000 tosses. That is, the result is closer to 0 than to 1. Nonetheless, it is possible to get 10 consecutive heads. The Fundamental Formula of Gambling calculates what the degree of certainty is to get 10 consecutive heads in a number of trials. Just run that astonishing probability software of mine, SuperFormula.EXE.
 Read Ion Saliu's first book in print: Probability Theory, Live!
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Founded on valuable mathematical discoveries with a wide range of scientific applications, including probability theory applied to gambling, lottery, sports, life, software.
Resources in Theory of Probability, Mathematics, Statistics, Combinatorics, Software
See a comprehensive directory of the pages and materials on the subject of theory of probability, mathematics, statistics, combinatorics, plus software.

| Home | Search | New Writings | Odds, Generator | Contents | Forums | Sitemap |
