
FFG Median, Skips, Lottery, Lotto Filtering, Probability, Odds, Jackpot
Playing Combinations around the FFG Median Can Improve the Odds of a Lotto Jackpot
By Ion Saliu, Founder of Lottery Mathematics

Published on February 17, 2002; later updates.
I come back to the idea presented in a previous article:
Dynamic versus Static in Lotto, Lottery Analysis.
I ran my lottery software Combinations to generate ranges of combinations around the field's midpoint or around the probability median for a 6/69 lotto game.
I applied the test to PA 6/69 lotto game (a very tough game, indeed; the jackpot odds are 1 in 119,877,472). I generated first 1000 combinations around the mid-point index: 59,938,736. That is, the lotto program generated combinations between the counts of 59,938,236 and 59,939,236.
Next, I checked for winners in the output file against real draws in PA 6/69 lotto (350 real lottery draws at my discretion). The mid-point output achieved 3 5 of 6 hits and 140 4 of 6 hits. The game odds are 1 in 317,000 for 5 of 6 and 1 in 4092 for 4 of 6. The 5 of 6 wins were recorded in 350 x 1000 = 350,000 combinations. Therefore, the mid-point strategy was about 3 times better than random play in the 5 of 6 situation. For the 4 of 6 case, 1 in 4092 applied to 350,000 lotto combinations translates into 85. The mid-point strategy hit 140 times, or about one and a half times better.
The next test was applied against the FFG median, instead of the mid-point. The FFG median is calculated in FFG for a degree of certainty DC equal to 50%. The FFG median is 83,092,731 for a 6/69 lotto game. A number of 1000 combinations were generated in the 83,092,231 83,093,231 range. The results were undoubtedly better. The strategy yielded 6 5 of 6 hits and 238 4 of 6 hits. Compared to purely random play, the FFG median strategy was 6 times better for 5 of 6 and about 3 times better in the 4 of 6 case.
I saw in the newsgroups similar tests applied to UK 6/49 lotto game, with lower odds than Pennsylvania's 6/69 monster lotto. This time, the results were inverted: the mid-point strategy was favored! It became clear to me that this type of lottery strategy favors the probability (FFG) median in high odds games. The higher the odds, the better the FFG median strategy fares.
I did the test for 10000 lotto combinations against the same 350-draw data file (PA 6/69 lotto). I ran the test for both the midpoint and FFG median: 5000 below and 5000 above (actually, there are 10,001 lotto combinations, including the pivots). The results were dramatic!
1) The midpoint strategy performed worse than in the 1000 test; even worse than random play! It recorded 6 5 of 6 hits and 442 4 of 6 wins. That's about half of what lotto random play yields!
2) The probability median strategy was far better than the 1000-combination test and far-far better than random play.
- 1 6 of 6 (jackpot) win (34 times better than random play);
- 75 5 of 6 hits;
- 2,232 4 of 6 wins!
Again, a random play for an equivalent amount of combinations (350 x 10001 = 3,500,350) should yield:
- 0.029 6 of 6 hits;
- 11 5 of 6 hits;
- 855 4 of 6 wins.
I compared these results with the results in a 6/49 game (UK, 642 draws).
The 10,001 runs did not yield jackpot wins. The lotto jackpot hits occurred at 50,001-combination runs!
1) Midpoint strategy:
- 27,439 hits (1 6 of 6 jackpot hit)
2) FFG median strategy:
- 34,616 hits (2 6 of 6 wins).
Now, the FFG median strategy was favored over the midpoint strategy!
It is very clear that this type of play favors the high odds games lotto by far. The lottery strategy is insignificant for lower odds games, such as pick-3 or pick-4 lotteries. I don't have a formula for it. I don't think this type of strategy has an under-pinning formula. The explanation relies on the type of combinations in various areas of the lotto field. The combinations in the FFG median area are largely part of the bell distribution. On the other hand, the purely random field includes many hardly-to-come-out-in-a-lifetime combinations. Combinations like 1-2-3-4-5-6 and the like, or 44-45-46-47-48-49 and the like.
Yes, some dudes will jump off: "They have an equal probability to come out!" But they won't come out equally (statistically). One can bet the entire budget surplus of the U.S. treasury in 2000 on lotto combinations such as the above. The results would be the red figures of the year 2002. I can give you here a summary explanation, other than the Markov Chains. The lotto balls would need to be mixed for millions of hours before any drawing. Then, weird combinations would have a reasonable chance to come out. It is all about number of trials N.
Probability is viewed by many as a static phenomenon. "The individual probability in the pick-3 lottery is 1/1000. Therefore every lottery combination has an equal chance of appearance." That's correct, insofar as no dynamic processes are involved. But the lottery is a dynamic process. There is more to the picture than meets the eye. The formula of individual probability becomes just a part of inclusive systems (formulae).
I have found out that many random processes are ruled by the Fundamental Formula of Gambling (FFG). Equal individual probabilities do not lead to equal frequencies. The pick-3 combinations do not appear equally. There are 1000 possibilities in the pick-3 game. In 1000 tries, each and every combination should come out, right? NOT! FFG shows that only around 63 percent of the pick-3 combinations come out in 1000 draws, any 1000 consecutive draws. Some 37% of the pick-3 combination need more than 1000 draws to come out: 1500 draws, 3000 draws, even 6000 lottery drawings!

- Let's answer a very interesting question. What is the probability that ALL pick-3 combinations will come out in 1000 lottery drawings (tries)? This point is closely related to the Classical Occupancy Problem and Probability of Collisions or Duplication (e.g. Birthday Paradox).
- Let's start with the simplest gamble: coin tossing. The probability is 1/2. Then, what is the probability that heads and tails will come out in 2 tosses? We apply the Binomial Distribution Formula. You can use my Super Formula to do the calculations. The probability for either heads or tails to come out EXACTLY once in 2 tries is: 1/2 or 50% (no surprise there). We must have EXACTLY 1 heads and 1 tails in 2 tosses. That is, ½ x ½ = Ό (25%).
The chance to get EXACTLY 1 heads AND 1 tails in 2 tosses is 1 in 4. The event will be heads-tails or tails-heads. It means that if we toss the coin 2 times, and do such a thing 4 times, we can expect to get a result such as heads-tails or tails-heads. Sometimes, we may get it in the first try of 2 tosses; other times, we may have to wait 10 or more 2-toss tries.
- Let's take a higher odds game: rolling the dice. A cube has 6 point faces. What is the probability to get ALL 6 point faces in 6 rolls? The individual probability is 1/6. We apply again the Binomial Distribution Formula. The probability to get EXACTLY 1 face point in 6 tries is 0.4 (40%). That chance is equal for each point face. The final result for ALL 6 point faces in 6 rolls is 0.4 to the power of 6: 0.4 ^ 6 = 0.004, or 1 in 250. We need to repeat the 6-roll event 250 times to get ALL 6 point faces in 6 rolls. Sometimes it can happen in 10 or 100 tries; other times, it may take 500 or 1000 or more 6-roll tries.
- The pick-3 lottery results enter the astronomical realm. We can't even say those numbers. The individual probability is 1/1000. We apply again the Binomial Distribution Formula. The probability to get EXACTLY 1 pick-3 combonation (a favorite of mine!) in 1000 lottery drawings is 0.368 (36.8%). It is a pretty high probability. That chance is equal for each pick-3 combination. The final result for ALL 1000 pick-3 lottery combinations in 1000 drawings is 0.368 to the power of 1000: 0.368 ^ 1000 = my-calculator-can't-compute-that-operation number! Raising only to the power of 100 gives 0.44 zeros3844! Forget about it! There is a far, far, far better chance for the Earth colliding with an asteroid that would put an end to all life.
- Undoubtedly, the lotto combinations have different frequencies as a matter of truth. Some repeat, some repeat more often, some do not appear at all in various ranges of trials. The process is not blind. It can be analyzed scientifically. As far as I am concerned, the Fundamental Formula of Gambling (FFG) has provided the best analytical tools. Its fundamental discovery: In 50% of the cases, each combination repeats after a number of trials less than/equal to the probability median of the game. That's a law. It is validated in any game of chance, lottery included. I analyzed the facts in other essays; e.g. Comparison of lotto software programs.
- I showed that in a lotto 6/48 (or 6/49) game, every number will repeat within 6 drawings in over 50% of the situations. Let's dig deeper into this statement. So, the probability of a lotto 6/49 number to repeat is 1/2 times 1/6 (the number will repeat after 1, or 2, or 3, or 4, or 5, or 6 drawings). The combined probability is 1/2 x 1/6 = 1/12. Actually, it is 0.54 * 1/6 = 0.09. But the lottery draws 6 numbers, therefore the probability to get all 6 numbers repeating after 1 to 6 drawings is: 0.9 ^ 6 = 0.000000531 (raising to the power of 6). The result can be expressed also as 5.31 times in 10 million, or 1,881,676 to 1. Well, the odds are better than playing 6 random numbers (1 in 13,983,816): 7 and half times better. That's a law.
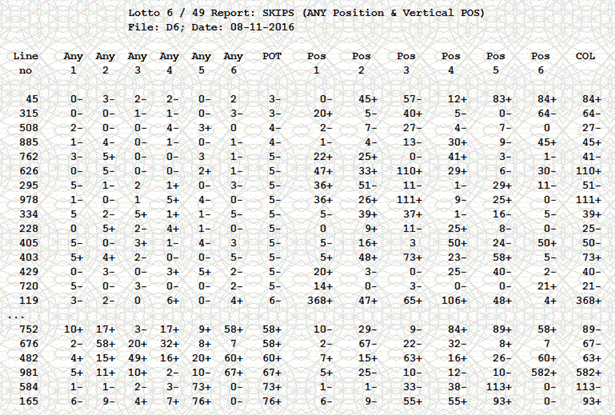
- You can have my peerless lotto software (LotWon or MDIEditor Lotto) create the well-known skip charts. Simply selecting 6 lotto numbers that show as current skips figures between 0 and 5 improves your lotto 6/49 odds sevenfold! There is no doubt or mystery here. It is a formula-backed fact. No matter when you play such a lotto strategy, your odds will always be seven times better than purely random play.
- Look at this real-life case (6/49 lotto in Pennsylvania Lottery). You can see that all skips are 5 or under in 14 drawings out of 1000 draws analyzed. You can improve the odds further if considering skips of 0 to 6 (20 additional winning situations). Meanwhile, I haven't seen one single draw where all 6 skips are in double digits.
- But look how much further we can improve the strategy by making sure that at least one skip is 0, while the rest of the skips are less than or equal to the median. It occurs 13 times (just one drawing shorter). A skip of 0 here means hits in consecutive draws. In the SkipSystem application, a hit in consecutive drawings is represented by a skip of 1 (in order to avoid few inaccuracies in roulette).
- It gets even better: At least 2 skips are 0, while the rest are less than or equal to the median. The amount of numbers in the pool to play is reduced dramatically. This strategy hits 12 times in 1000 drawings - not a big drop in strategy hits from 14 without the new restriction.
- The flipside: There is NO software to apply this strategy exactly. We can only get a string (pool) of numbers with skips under FFG median; e.g. 25 numbers in 6/49 lotto.
- Only the lexicographic generator in SkipDecaFreq6 can generate combinations for such situations: Screen_1, the Any and Pos filters. The maximum levels of all Any filters are set to 6.
- Save the combinations (e.g. C(25, 6) = 177100) to an output file.
- If 2 of the maximum Any filters are set to 1, we would deal with only 200020000 combinations. They can certainly be LIE eliminated further safely.
- Purge the output file (of 177100 combos) in Lexico6 (function L in main menu) by setting the maximum level of the Two filter to 1.
- This is only an approximation at this time and there is no alternative.
You might have to wait a lifetime or two to see all skips larger than 20! Well, then, why play lotto numbers that all have large skips?! Random selection can include many lotto numbers with very large skips. And that is the reason why random play fares clearly worse than playing lottery numbers with skips less than or equal to the probability (FFG) median. None of 1000 lottery drawings analyzed in Pennsylvania Lottery had all skips in double digits. See the real-life statistical report: Report: Lottery Skips Systems, Best Chance at Lotto Jackpot.
The cynics who ragingly cry that the odds are always the same are right once and only once. At the very beginning of the lottery game, all skips are "equal": 0 (zero). The skip-charting lottery software is Skip Decades Frequency, menu II of the Bright / Ultimate Lottery Software packages, function S = Skips, Decades, Frequencies. The report is sorted in ascending order by the POT column (representing the largest skip in a 6-number drawing).
- Inquisitively axiomatic reader and student of randomness, a point is in tall order: House edge or house advantage (HA). We all know that lottery, unlike casino gambling, enjoys (imposes, in fact) a huge, humungous HA. We calculate the house advantage with another formula based on units paid UP over total possibilities TP:
HA = 1 (UP / TP)
(Always expressed as a percentage.)
- If, par exemple, the 6/49 lotto game has a 2-million units (e.g. dollars) in payout for jackpot, and total combinations reach about 14 million (to simplify):
HA = 1 (2/14) = 85.7%.
- Granted, the jackpot has rollovers. Let's consider a nice case-scenario and set the average payout to 4 million dollars. The lottery house advantage is still big: 71.4%. By contrast, the house edge in the American roulette is 5.26%, or 13 times better!
- The player can have an advantage, however. If the payout exceeds the odds (total possible outcomes), that is a disadvantage for the house (the lottery commission). For example, if the payout (jackpot) is over 14 million, the player has an advantage. Qualification: If the player chooses to play only when the lotto jackpot is over 14 million dollars (units). Of course, it would take many, many drawings for that player's advantage to come to fruition (biblical lifetimes!)
- Things get better (shorter lifespans) if we apply the discovery above: Play only lotto numbers with skips under the FFG median. Total possible outcomes go down to 1,881,676... let's make it 1.9 million. If the lottery player only plays when the jackpot is equal to or above 2 million pay-units. The minimum player advantage turns out to be... 5.26%. The best roulette out there as far as players are concerned!
- Evidently, the lotteries would die if players choose to play only when they have an advantage. There wouldn't be enough players to push the jackpot amount over the advantage limit. Actually, there wouldn't be a jackpot at all! In casino gambling, the player must play every bet. However, the mathematical gambler can bet bigger when the degree of certainty is higher. Such gambling strategy offsets losses in minimum-bet situations.
As for the midpoint and FFG median strategies presented at the beginning of this post: I do not endorse them. I have no formula to lay a foundation. They might as well be expensive to play. They certainly need further lotto filtering, using LotWon filters. You should never ever apply ordinary cigarette-butt filters to smoking down the lottery odds!

Resources in Lottery Software, Strategies, Lotto Systems
- The Main Lotto, Lottery, Software, Strategy page
Presenting software to create free winning lotto, lottery strategies, systems based on mathematics. Get your lotto systems or wheels, the best lottery, lotto software, combinations, winning numbers.
- Lotto, Lottery Software, Excel Spreadsheets: Programming, Strategies.
Read a genuine analysis of Excel spreadsheets applied to lottery and lotto software development, systems, and strategies. Combining Excel analysis with powerful lottery and lotto software programmed by this author, Parpaluck.
- MDIEditor Lotto WE: Lottery Software Manual, Book, ebook, Help.
~ Also applicable to LotWon lottery, lotto software; plus Powerball/Mega Millions, Euromillions.
- Visual Tutorial, Book, Manual: Lottery Software, Lotto Apps, Programs.
- Skip System Software: Lotto, Lottery, Powerball, Mega Millions, Euromillions.
- Optimizing the Skip Systems in Lottery, Lotto, Gambling, Horse Racing.
- Lottery Utility Software: Pick-3, 4 Lottery, Lotto-5, 6, Powerball, Mega Millions, Thunderball, Euromillions.
- Lotto Filters, Reduction Strategies in Lottery Software.
- "The Start Is the Hardest Part": Play a Lotto Strategy, Lottery Strategies; Work with Data Files.
- Artificial Intelligence AI, Axiomatic Intelligence AxI, Neural Networks in Lottery: Strategies, Systems, Software.
- A Practical Essay on Artificial Intelligence, AI Chatbots Regarding Ion Saliu.
- Lotto wheels for lotto games drawing 5, 6, or 7 numbers.
The most advanced theory of lotto wheels or reduced lottery systems. Get also original lotto wheels for lotto games drawing 5, 6, or 7 numbers: Balanced, randomized, and free.
- Download lottery software, lotto software.

Home | Search | New Writings | Software | Odds, Generator | Contents | Forums | Sitemap








