
Theory of Filters, Filtering, Reduction in Lotto, Lottery Software
By Ion Saliu, Founder of Lottery Filter Mathematics




I. Introduction to Lottery Filters and Filtering in Software
II. Setting the Lottery Filters: Theory and Software Tools
III. More Advanced Theories in Setting Filters and Lottery Strategies
IV. Older Writings in Setting Filters; Lottery Software Users Creating Strategies
V. Resources in Lotto, Lottery, Software, Filters, Strategies, Systems
The lottery filters are parameters that eliminate combinations in the generating processes by the LotWon lotto and lottery software. In other words, the filters are restrictions. One simple restriction, as an example: Generate lotto combinations that do not repeat any past drawing that hit the jackpot.
Ironically, mostly the minimum levels of the lottery filters are perceived as... filters! Actually, the filters in my lotto software had only minimum levels for years. That's how it started. It took me many years to realize that there is no minimum without maximum. Reason: The personal computers in the 1980s were not advanced. And another reason: I evolved as a programmer.
Both levels of a filter are equally efficient. There are no universal formulas to calculate the efficiency of lottery filters. By efficiency, we mean the amount of lottery combinations that a filter eliminates.
Let's say the lotto game consists of 6 winning numbers per drawing. We can calculate exactly, by formulas, how many combinations the filter ONE would eliminate and the filter SIX — But only if we set each level to 1. That is, the calculations can be performed only if we consider one past drawing as a filter setting. That's because groups of lottery numbers do repeat — also according to probability theory.
The minimum level of filter ONE (the name is just intuitive) eliminates all single-number groups from past lotto drawings. If we set the minimum level of the ONE filter to 1, it will eliminate EACH lotto number from the previous draw. There are 6 numbers per combination. Thus, we will eliminate 6 numbers from the field of play (e.g. 49 numbers in the game). Only numbers from the remaining 49 – 6 = 43 lotto numbers will be part of the combinations generated.
Therefore, the minimum level of ONE will allow an amount of combinations equal to the formula of combinations 43 taken 6 at a time. C(43, 6) = 6,096,454 combinations. Total number of lotto combinations C(49, 6) = 13,983,816. In other words, the minimum level of ONE will eliminate 7,887,362 combinations.
The maximum level of ONE does the opposite. If the maximum level of ONE is set to 1, it eliminates 6,096,454 combinations. Equivalently, it allows 7,887,362 lotto 6/49 combinations.
The other filter we can apply formulas to is a lotto parameter we could call SIX. It will apply only the complete 6-number groups as a restriction. We set the minimum level of SIX to 1 (the previous drawing only). There is only 1 possible 6-number group to match the past draw. This minimum level of SIX will eliminate exactly one lotto combination. The opposite: The maximum level of SIX will allow exactly one combination (i.e. it eliminates the rest of the combinations in the lotto game).
There are no formulas for other types of restrictions or lottery filters. The only way to determine the efficiency of a lottery filter is by running the software in lexicographical generating mode (L in the main menu of Bright / Ultimate Software). Set the minimum level of a particular filter to 1. Write down how many lottery combinations were generated. Set the maximum level of a particular filter to 1. The result should be the complementary of the amount of combinations generated by the minimum level. That is, if you add the amounts of lottery combinations generated by the two levels of the same filter, the result should be equal to total number of sets in the lottery game.
You might want to save to a document the efficiency figures for every filter in your particular software packages. Print the document as a good reference to aid you with my lotto and lottery software.
Lotto filters such as Four, FivS, FivR have a special behavior. They are so high, that they reach levels beyond a small data file. If you analyze 10,000 draws, FivS in layer 1 shows 10,000. Most likely the filter is higher than that. It can reach over 20,000, I know it for a fact. In my lotto 6/69 game, both FivS, and FivR reached 100,000 easily. That's why the FivS, and FivR filters do NOT have maximum levels! The Four filter has a maximum level, but it requires caution. If the filter shows 10,000 in your WS6.1 report, it simply means there weren't enough draws to analyze.
You can use the WS files and the QEdit editor (it does NOT work in 64-bit Windows). QEdit has some nice features I did not bother to implement in my editors. Why should I reinvent the ... lotto wheel every time?!
One nice feature of QEdit is column block or column selecting. Read the manual for the shortcut, it probably is Alt+k. Go to the first drawing in the WS file. Move the cursor to the first digit of a filter (column). If a lotto software filter has four digits, make sure the cursor is four spaces from the rightmost digit. The column block must cover all the digits in the filter. Press simultaneously Alt+K then press the right arrow key until you reach the last digit in the column. Press the down arrow key until you reach the last line in the WS file.
Here is a screenshot of the folder organization:
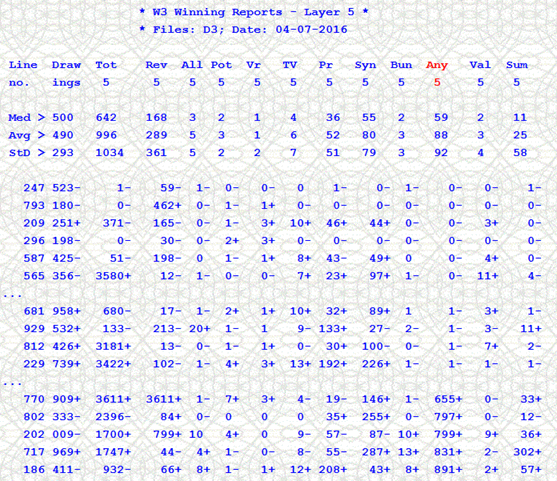
There are lots and lots of reports!! The more reports the higher the chance to come up with a large number of efficient strategies. It took me a couple of hours to generate the winning reports, sort all of them on all filters and finally move them to the StratSorRep subfolder for each of the Ultimate Software packages. I had a couple of glasses of wine to make the tedium less "oppressive"! Virtually, the sorted reports will be good forever.
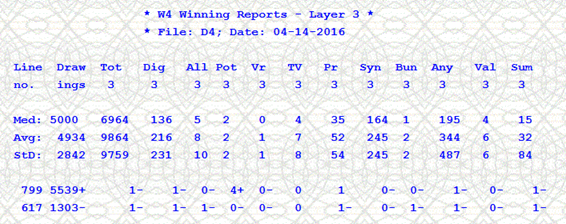
The sorted reports show the lowest filter figures at the top, while the largest column values go to the bottom. The report is ordered by the Any_5 filter. I had once good success (when I played the lottery in earnest!) I set Any_5_minimum = 400. Sometimes, the strategy would not generate a single combonation. I mixed and matched Any strategies from various layers in case one strategy was in a "slump". The strategies go "cold" at times, and get "hot" at other times. But them all lottery strategies have skip medians that are mathematically consistent.
So, when I say wacky filter values I mean the top and the bottom of a sorted winning report for the key column. Of course, we always should set other filter values at runtime. We can see here that when Any_5_minimum = 400, other filters are usually non-zero (Tot, Rev, Pr, Syn, Sum). We can play aggressively and set Tot = 1000 as it occurs 14 times with Any = 400. And, certainly, we can also combine filters from different layers and from different programs.
We can also work with filter values in the median area of the sorted winning reports WS. In this third type of lottery strategy, we can set tight filter settings. In this particular example, we can see in the reporty heading that the median is equal to 59. We can select Any_5_minimum = 59 AND Any_5_MAXimum = 60. This setting might be so tight that no combination will be generated sometimes. We can loosen it up with a setting like: Any_5_minimum = 58 AND Any_5_MAXimum = 62
For example, if a median is 12, you can set a tight lottery filter to 12 * 4 = 48 (or rounded up to 50) for the minimum value of the filter. Or, you can set an equally tight filter to 12 / 4 = 3+1 for the minimum value of the respective filter. (Remember, the maximum level of a filter must be at least (minimum level + 1). If a filter is set to 4 times the median, it slashes in half four times the total combinations. In the pick-3 lottery game example: 1000 lottery combinations reduced to 500 in the first step; 500 slashed to 250; 250 halved to 125; finally, 125 reduced to 60+.
A sorted-by-column WS file can show you even more valuable information. Say, you sorted W3.1 by the Pairs-1 column. The median was 32. The median divided by 4 = 8. Go to line 1 of the column and see how many Pairs-1 are lower than 8. You can see also what kind of levels other filters show for Pairs-1 less than 8. Other filters may show very low numbers as well. Other lotto filters may show bigger numbers. You can choose as a playing strategy Max_Pair_1=8+1=9, plus other filters at less tight levels. For example, Max_Vr_1=4, Max_TV_1=6, Val_1=5. This is just an example. You can find similar numbers in your sorted WS files.
The median multiplied by 4 = 128. Go to the last line of the column and see how many Pairs-1 are larger than 128 (or 120 or 130; you can round up or down for more flexibility in your choices). You can see also what kind of levels other filters show for Pairs-1 greater than 128. Other filters may show very high numbers as well. Other filters may show lower numbers. You can choose as a playing lottery strategy Min_Pair_1=130, plus other filters at less tight levels. For example, Min _Vr_1=1, Min _TV_1=5, Min_Syn_1=50.
Using such tight levels for one or very few lotto filters eliminates a huge amount of lotto combinations. Such levels occur more rarely. You should not play them in every drawing. They skip a number of drawings between hits. The newest pick-3 software makes it even easier for you. The application has also a strategy checking software utility. It shows the levels of all the filters and the skip chart of the strategy.
Please read also the Pick-3 Lottery Strategy, System, Method, Play, Pairs page. It shows why you should only play a strategy if its current skip (the first number in the skip chart) is less than or equal to the median. For example, if the median of the strategy is 5, you should play it only if the first number in the string of skips is 0, or 1, or 2, or 3, or 4, or 5. If the current skip is larger, don't play the strategy; save the money. Since you can select a very, very large number of lottery strategies, look for another strategy. Look for a strategy that shows a current skip under the median.
Again, the pick-3 lottery software makes it easier for you. It shows more evidently the filter movement. When a filter is higher than in the previous drawing, the filter has the + sign at the right. If the filter is lower than in the previous draw, it has a - sign attached. It is more visible. You can notice that in most cases the filters go from one trend to the opposite after two or three drawings. That is, after 2 or 3 + signs, the - sign comes up; or vice versa. Based on that, we can look at each filter (column) in the WS files.
The key position is line #1. If the sign in line #1 is -, and also in line #2, and line #3, (3 decreases in a row), we should expect a + (increase) the very next draw. If the sign in line #1 is +, and also in line #2, and line #3, (3 increases in a row), we should expect a - (decrease) the very next draw. Let's take pick-3 lottery as an example. Pair-1 in line #1 is 12 and it shows -, the 3rd consecutive - (decrease). We should expect a + in the very next drawing. An increase in a filter requires the use of the minimum level of the respective filter. In this example, I'll set Min_Pair_1=13. If I want to increase the probability, I can set Min_Pair_1=10, for example. Of course, the program will generate a larger amount of pick-3 straight sets.
Let's say now Pair-1 in line #1 is 123 and it shows +, the 3rd consecutive +. We should expect a - in the very next drawing. A decrease in a lottery filter requires the use of the maximum level of the respective filter. In this example, I'll set Max_Pair_1 = 124. If I want to increase the probability, I can set Max_Pair_1 = 130, for example. Of course, the program will generate a larger amount of pick3 lottery sets.
You can look for longer streaks, of either + or -. Just go the line #1 in each WS file. There are situations when the current streak can be 4-long, or 5-long, even longer in rare situations. You may want to consider first the longer like-sign streaks. Keep in mind, however, that the streaks shift direction after up to 3 drawings in most cases. Actually, streaks of 1 or 2 consecutive like-signs are the most frequent. I will not go any further in this direction.
You can combine filters selected as in this path with the type of selection presented in path #1. You can set one tight filter (4 times the median, etc.). Then you set other filters as in path #2. For example, Min_Pair_1=120 (path #1), Max_Vr_1=7 (path #2), Min_TV_1=10 (path #1), Min_Syn_1=100 (path #1), Max_Bun_2=6 (path #2), Max_Tot_3=1500 (path #2), Max_Any_5=300 (path #2). And so on…



1) the range of analysis is too short (100 lottery drawings or so);
2) a very low number of past lottery draws to use (way below 100,000).
And one more reason is an insufficient number of layers. The number of layers can be increased only by increasing the number of D* files.
There is that much-talked-about ION5 filter, in both MDIEditor and Lotto and in the LotWon (Command Prompt). The filter is constructed absolutely the same way. That lotto filter can reach the skies, literally. It can grow huge, if the D* file goes above 100,000 combinations. For a 6/49 lotto game, ION5 can reach TOTAL_DRAWS/24. (BTW: 24 = INT(49/2)). If no Ion_5 is above 4,167 in a 100,000-line D6 (MDIEditor file) or a layer in DOS Pick632, then that data file of yours is probably of a sufficient size. For a 5/39 game, ION5 can reach TOTAL_DRAWS/20. If no Ion_5 is above 5000 in a 100,000-line D5 (MDIEditor file) or a layer in Bright5, then your D* file is probably of a sufficient size.
Yet, the wackiness can go above those figures. I exemplify by my lotto 5/39 game. I generated all the lotto combinations in the game (575,757) by running that great piece of combinatorial software PermuteCombine. Next I shuffled the all-5-39 combo file by running that great application Shuffle. I shuffled once and thus created my first SIM-5 file. I shuffled the all-5-39 lotto file a few more times, creating every time a different SIM-5 file.
I have seen Ion_5 of 2500+, 5000+, 6000+, 7000+… Those are scary numbers… scary not to you, but to the odds! I did a few tests with min_Ion_5 = 2500. Well, for a majority of the cases: there is no output; no combinations generated, even if the inner filters are disabled.
I checked for a situation when ION5 was over 2500. I generated lotto combinations in lexicographical order. Total combinations generated: 1 (ONE), both with the innate filters enabled and disabled. You know, I like that! Had I figured it out five years ago, I would have hit the 5/39 lotto jackpot a dozen times or so. Granted, my PC of 5 years ago was kinduva snail (300 MZ PII).
So, now I take a look at wacky-wacky lotto filters, such as the storied Ion-5. If it isn't over 2500 in a layer, look at another layer… or look at another D* lottery data file. Wackiness is not the exclusivity of one layer or one drawings file. Wackiness repeats itself the same way that history repeats itself.
Indeed, there is the need to present more facts on the filters in LotWon software. The documentation in SuperPower lottery software does not cover how to use the maximum values of the filters.
The minimum value of a lottery filter is equivalent to at least. If we choose Two-1 = 3, we'll be correct if Two-1 was at least 3 (shown in the W6 files). That means, 3, 4, 5, ... 10, 11, etc. We would be losing if Two-1 was 2, or 1, or 0.
The maximum value of a filter is equivalent to no more than but not equal to. If we choose Max_Two-1 = 3, we'll be correct if Two-1 was no more than 2. Pay special attention to this: the maximum must be at least the minimum plus 1. We would be correct if Two-1 was 2, or 1, or 0 (shown in the W6 files). If Two-1 was 3 or more, that would be a losing situation.
If the W6 files shows 0 for Two-1 we can only play the maximum value for the lottery filters. Playing the minimum value will have no effect (since it is equal to 0). In this case, the correct entry for Max-Two-1 is 1 (0+1=1).
The effect of a filter depends on the lotto game format. I will exemplify the effect of some filters for the lotto 6/49 game. It is the most popular around the globe and I received a real-life W6 lotto report (from the user named Guy). I will not accept any W6 files to look at any more.
1) Let's see how many lotto combinations the minimum value of the filter Two eliminates if we set it to 1. A 6-number winning combination can be broken down into C6 taken 2 at a time C(6, 2) = 15 combinations. There are 49-6=43 remaining lotto numbers. The 43 remaining numbers can be broken down into C43 taken 4 at a time = 123410 combinations of 4 lotto numbers each. Each of the 15 2-number lotto combinations can be attached to each of the 123410 4-number combinations. The result is 15 x 123410 = 1851150 total 6-number lotto combinations. Therefore, the filter Two = 1 eliminates 1,851,150 combinations.
Let's make Two = 2. It means we eliminate all two-number combinations from the last two drawings. If the two past lottery drawings have no common numbers, the filter Two = 2 eliminates 1,851,150 x 2 combinations. If Two = 3, the filter should eliminate 1,851,150 x 3 combinations. And so on? NOT! In reality, some pairings (two-number lotto groups) are a lot more frequent than others. Some lotto pairings do not come out even within 200 drawings. So, the effect of Two diminishes after two or three past lottery drawings. I also recommend the use of the Least 6 file: the file with the least frequent pairings in a lotto game.
If the filter Three is set to 1, it eliminates all three-number groups from the most recent lotto drawing (the previous one). C(6 taken 3 at a time) = 20 combinations. The 43 remaining numbers can be broken down into C(43 taken 3 at a time) = 12341 combinations of 3 numbers each. Each of the 20 3-number lotto combinations can be attached to each of the 12341 3-number combinations. The result is 20 x 12341 = 246820 total 6-number lotto combinations. Therefore, the filter Three = 1 eliminates 246,820 combinations.
Let's make Three = 2. It means we eliminate all three-number combinations from the last two drawings. If the two past drawings have no common numbers, the filter Three = 2 eliminates 246,820 x 2 lotto combinations. If Three = 3, the filter should eliminate 246,820 x 3 combinations. And so on? NOT! In reality, some three-number combinations are a lot more frequently than others. The Three filter will diminish its eliminating power after some 10 past lottery drawings.
2) Let's see how many combinations the maximum value of the filter Two LEAVES TO BE PLAYED if we set it to 1. A 6-number winning combinations can be broken down into C(6 taken 2 at a time) = 15 combinations. There are 49-6=43 remaining numbers. The 43 remaining lotto numbers can be broken down into C(43 taken 4 at a time) = 123410 combinations of 4 numbers each. Each of the 15 2-number combinations can be attached to each of the 123410 4-number combinations. The result is 15 x 123410 = 1851150 total 6-number combinations. Therefore, the filter MAX_Two = 1 LEAVES 1,851,150 combinations to be played. In other words, the lotto software will generate 1,851,150 combinations.
Let's make MAX_Two = 2. The calculation is different now. Suppose the last two lotto drawings have no common numbers. Thus, the last two drawings consist of 12 unique numbers. C(12 taken 2 at a time) = 66 combinations. There are 49-12=37 remaining numbers. The 37 remaining numbers can be broken down into C(37 taken 4 at a time) = 66045 combinations of 4 numbers each. Each of the 66 2-number combinations can be attached to each of the 66045 4-number combinations. The result is 66 x 66045 = 4358970 total 6-number lotto combinations. Therefore, the filter MAX_Two = 2 LEAVES 4,358,970 combinations to be played. But the disclaimer above still applies and even widens the discrepancy.
If the filter Three is set to 1, it LEAVES TO BE PLAYED all three number combinations from the most recent lotto drawing (the previous one). C(6 taken 3 at a time) = 20 combinations. The 43 remaining numbers can be broken down into C(43 taken 3 at a time) = 12341 combinations of 3 numbers each. Each of the 20 3-number combinations can be attached to each of the 12341 3-number combinations. The result is 20 x 12341 = 246820 total 6-number lotto combinations. Therefore, the filter Three = 1 LEAVES TO BE PLAYED 246,820 combinations. But beware of the phenomenon described for the case of Two.
Looking at the W6 files from Guy, I saw Two of 20 or more. That's a high value for the minimum value of the lottery software filters in this category (Two or 2-#s). Such a high value has corresponding high values for other filters (Three or 3-#s and Four). Using such high values for some filters will eliminate a huge number of lotto combinations.
In the same reports, I saw Three filters of 150 or more. Such high values for the minimum entry of Three also eliminate a huge amount of lotto combinations. Also, Four of 2000 or more (even 4000) and Sum of 400 or more (even 700) do eliminate millions of combinations.
You will notice that high values for one filter are correlated with high values of other filters. But these high values occur from time to time, not very frequently. You will skip some lotto drawings in between situations of high values for the 'minimum' level of the filters. As in Guy's reports, in drawing #20, the filter Sum-1 was 828, then in drawing #13 it was 469. So, we played once setting Sum-1 = 400 for the minimum level, then skipped 5 lotto drawings and played again Sum-1 = 400. We would have lost 2 drawings, but had another winning situation in drawing 13.
In reverse, efficient maximum levels of the lotto filters are LOWER ones. For the Two filters, 0 is the most efficient value and it occurs quite frequently (more than 15 times in 100 drawings analyzed by Guy). In such cases, you set MAX_Two-1 = 1. There are also situations are 0. For example, you set MAX_Two-1 = MAX_Two-3 = 1. The effect is quite dramatic: a substantially lower number of combinations will be generated. Or even more dramatically, you can set all six Two filters to no higher than 5. Thus, MAX_Two-1 = MAX_Two-2 = MAX_Two-3 = MAX_Two-4 = MAX_Two-5” = MAX_Two-6 = 6.
For the filter Three, an efficient level of the maximum would be 5. For the filter Four, you can set the minimum = 50 and MAX_Four = 100.
From all these facts, you can deduce that there are values UNUSUALLY high or UNUSUALLY low that occur from time to time in your W6 files. Therefore, we can set highly efficient filters and expect to win with substantially fewer lotto combinations from time to time.
If you want to generate the winning lotto combinations every time you run WHEEL-6, you need to set SAFE values for the filters. The selection of safe values is not 100% guaranteed, but it is not rocket science either. You should not expect to select the right levels of the filters every time you run the programs.
You can notice in your W6 files that usually high values are followed by lower values (or vice versa). Normally, three increases in a row are followed by a decrease (or vice versa: three decreases followed by an increase). For example, in Kulai's report, Three-1 was, in three consecutive lottery drawings, 191, 29, 12, followed by 31. I would have set Three-1 = 13 and MAX_Three-1 = 51 (an increase from 12 but no higher than 50).
Your accuracy in setting this type of safe levels of the lottery filters will increase with usage: the more you work with the W6 files, the less erroneous your filter-setting will get.
Resources in Lottery Software, Lotto Wheeling, Systems, Strategies
See a comprehensive directory of the pages and materials on the subject of lottery, lotto, software, systems, lotto wheels.
Pages dedicated to help, instructions, filters, strategies for the best lotto programs and lottery software in the world:

