
Random Numbers, Shuffle, Randomize: Theory, Algorithms, Software, Source Code, Generators
★ ★ ★ ★ ★
By Ion Saliu, Founder of Randomness Programming



Written by Ion Saliu on June 18, 2004; last update October 2012.
First captured by the WayBack Machine (web.archive.org) on July 7, 2004.
• RandomNumbers.BAS version 3.01 ~ October 2012 – Software, algorithms, source code for the BASIC programming language to generate true random numbers (far from pseudorandom numbers!)
There are four types of sets: exponents, permutations, arrangements, and combinations. I assume the original poster wanted to generate random combinations or random numbers for lottery (lotto combinations). In the case of the combination set, the random numbers are unique (per line) and also sorted in ascending order (per line). You can read a lot more about sets, and also get free software written in PowerBasic Console Compiler:
Combinatorics: Calculate, generate exponents, permutations, combinations - for any numbers and words.
The following is a fully functional program that runs in PowerBasic Console Compiler IDE (Integrated Development Environment). The source code uses two little-known algorithms to generate unique random numbers. The numbers are truly random. The randomization seed is highly random; therefore the next sequence of (set) of numbers is unpredictable.
The algorithms in this sample program are most concise algorithms of random number generation. There are numerous algorithms to generate random numbers or combinations. My software, for example, uses multiple techniques and algorithms (routines) to generate random numbers.
The computers can generate numbers as highly random as by manual selection or running mechanical devices. The first essential condition is the random seed. Using the computer timer results in lowly random generation. They call it pseudo-randomness. I did write far better seed generators for Visual Basic and PowerBasic PBCC.
The second essential condition for true random number generation is the SPEED of execution. The higher the speed, the lower the degree of randomness. The software takes an 18-digit floating-point number and generates the first random number (which is floating point, between 0 and 1). The software multiplies that number between 0 and 1 by the largest number in a lotto game (as an example). The calculation is very fast. The software generates quickly another floating-point random number and multiplies it again, etc. Because the calculations are extremely fast, the numbers generated tend to be close to their neighbors.
I remember way back when I used an Atari (very slow!) to generate random numbers. The degree of randomness was far higher than what the much faster PCs gave me. Now, delaying the random generation does improve the degree of randomness. My lottery software is not plagued by computerized pseudo-randomization because it performs up to billions of operations. The operations delay considerably the generating of combinations.
I noticed long ago that if the seed generation is inside the generating loop and there is no delay, the numbers tend to repeat or to be very close to each other. For, example generating randomly 6 lotto numbers from 1 to 49:
FOR Counter = 1 to 6
RANDOMIZE TheSeed
Lottonumber(Counter) = INT(RND * 49) + 1
NEXT Counter
But if I add a DELAY command just before the NEXT Counter command, then the randomization improves. Also the RANDOMIZE The_Seed command should be moved outside the loop (before FOR Counter = 1 to 6). Slowing down the generating procedure assures satisfactory random numbers.
Don't take randomness as being perfect. Randomness is random — that's all! As a matter of fact, everything is random, including the Universe as Totality. I was the first to demonstrate mathematically that absolute certainty is the pinnacle of mathematical absurdity. The Fundamental Formula of Gambling (FFG) proves undeniably that everything comes in degrees of certainty.
The delay in execution is also acceptable in these algorithms. The program divides the two random numbers and the result is compared to the RND result. The delay is just sufficient to make the numbers (lotto combinations) acceptably highly random. Nobody will be able to predict accurately the next sequence of lotto numbers.

And here is one more highly prized randomizing algorithm of mine. The algorithm very much resembles shuffling a deck of cards.
Again, 100% compatible with Power Basic Console Compiler (PBCC)...
'This routine generates unique random numbers to screen = SORTED
FOR ION = 1 TO GU
S2 = K
S1 = V
' the largest number, V, and numbers per combination, K
FOR j = 1 TO S1
IF RND < S2 / S1 THEN
PRINT j;
S2 = S2 - 1
END IF
S1 = S1 - 1
NEXT j: PRINT
NEXT ION
DIM N AS LONG
'total elements in the set to be shuffled
' e.g. N = 52 cards or N = 49 lotto balls
'create an array with all the elements from 1 to N
DIM X() AS LONG
REDIM X(N)
FOR I = 1 TO N
X(I) = I
NEXT I
FOR I = 1 TO N - 1
SWAP X(I), X(INT(RND * (N - I + 1) + I))
NEXT I
FOR ION = 1 TO GU
FOR I = 1 TO V - 1
SWAP X(I), X(INT(RND * (V - I + 1) + I))
NEXT I
FOR J = 1 TO K
PRINT X(J);
NEXT J
PRINT
NEXT ION

Included is a highly randomized function I created to set the random seed: TheSeeder. It uses the system date and time, instead of just the TIMER. Many confuse randomness for probability. If the seed is between 1 and 10, for example, the seed is not considered to be random. In fact, what we talking about is the DEGREE OF RANDOMNESS. The larger the range of the seed, the more randomized the seed is. That's so because the probability of selecting one particular seed is lower.
The TIMER takes 86400 values (number of seconds in 24 hours). of course, if using the TIMER only as the seed and running the random generator at the same time of the day, the sequence of numbers will be always the same. Hence, the term pseudo-random. TheSeeder() generates random seeds between millions and billions. You won't see the same seed again in your lifetime!
You can read a lot more about randomness: Almighty Number, Randomness, Universe, God, Order, History, Repetition.
Hope you'll find the Basic source code useful, albeit a little long. No error trapping was implemented. To avoid errors, make both parameters positive. The biggest "lotto" number must be larger than “numbers per combination”. If the two parameters are equal, one and only one sequence of randomly-generated numbers will be generated (e.g. 1 2 3 4 5 6 for N = 6 and M = 6).
The code requires changes when ported to other Basic implementations or other programming languages. That would be entirely your job, in case you speak a different programming language...
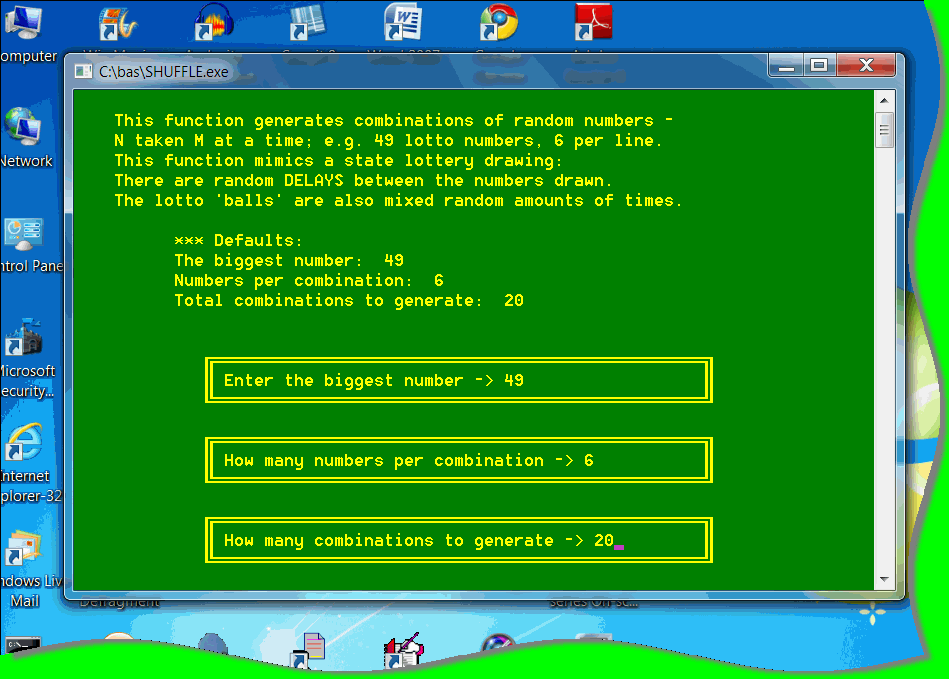
•• You can also download the compiled random number program, which is more potent: It adds a function that delays the random generation of numbers. The software mimics a lotto drawing conducted by the state lotteries. Program name: RandomNumbers.EXE. Software categories: 5.2 & 5.6 - accessible via the main download page.
The fully functional program can also generate roulette spins. The parameters: Largest number 37 (French roulette) or 38 (American roulette); numbers per combination = 1 (one spin at a time). Then deduct 1 from the outcome. Thus, roulette number 1 becomes 0, while 37 becomes 36. The special case in American roulette: number 38 becomes double zero (00).
OK, okay! There is also the question of verification. How can we verify that the numbers are truly random? Good question!
All events are random -- only the degree of randomness is variable. We can verify true randomness by applying Ion Saliu's Paradox of N Trials. A total of 1 - 1/e or 63% numbers are unique. Thus, if we generate N numbers, around 37% of them will be duplicates or repeats. For example, if we generate 37 roulette numbers, around 25 of them will be unique or non-repeats; 12 or so of the roulette numbers will be repeats from previous spins.
A little-known secret now. There is no… secret that the lotto combinations randomly generated will not hit with the first seed, or the first few randomizing seeds. Therefore, the more seeds the random-number generator uses, the higher the degree of certainty of getting closer to the winning lotto combonation. Thusly, let's generate several randomization seeds before generating random numbers (as in random lotto combosnations)! I am using here the number of repetitions somehow related to the golden number PHI:
So, we randomly generated from 1 to 1618 randomizing seeds, and then we start the random generating process via the BASIC program. To generate random roulette numbers (spins), enter 37 for single-zero or 38 for double-zero roulette. Numbers per combination (line): 1 (37 represents 0, 38 is for 00). To generate random coin tosses, enter 2 for the biggest number. Numbers per combination (line): 1.
The source code is no longer on this Web page. Version 3 is a lot more comprehensive. The new program incorporates both algorithms of random number generation. Therefore, I created two new Web items.
The first item is a standard HTML page where the code is posted between two PRE tags. You can copy the source code and paste it to your favorite programmer's editor.
The second item is actually a BAS file that can be downloaded directly, and then loaded into the compiler.
You can also download for FREE a zipped file that contains both the compiled program and the source code:
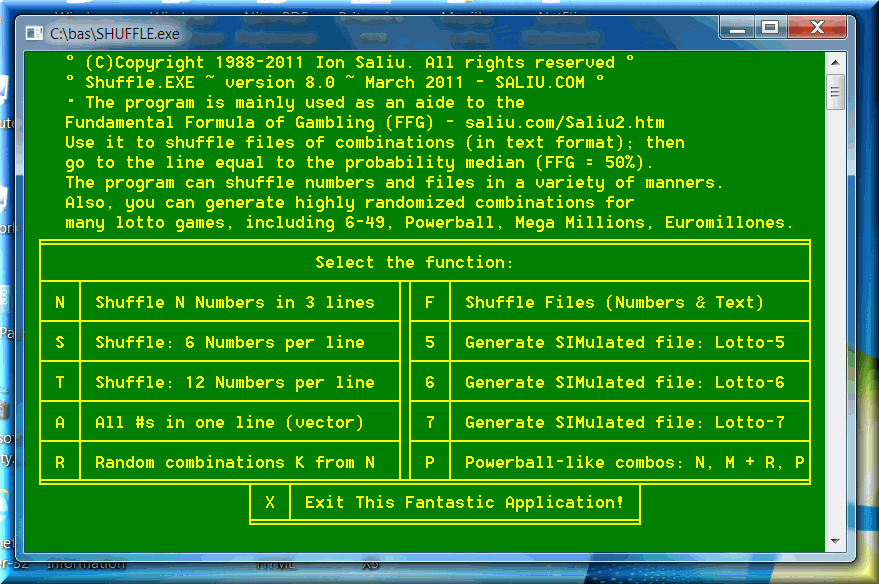
Instead of publishing the old source code of randomization, I present a potent piece of software that performs randomization at its best: Shuffle.The program can generate combinations for all kinds of lotto games, including Powerball, Mega Millions, Euromillions. The combinations tend to be like in real-life: the software generates unordered random numbers. The random generating processes can also be randomly delayed, as it occurs in lotto drawings conducted by lottery commissions (agents).
Shuffle is must-have software for all those with a strong interest in randomness in the field of computer science. There is no better program to generate true random numbers — possibly never will be!
FOR I = 1 TO RND(1, 1618)
TheSeed = TheSeeder ()
NEXT I
RANDOMIZE TheSeed


Randomness is the reason why God fears Mathematics, while Einstein hates gambling.
Only Randomness is Almighty. Randomness is great! Randominus vobiscum!
 Read Ion Saliu's first book in print: Probability Theory, Live!
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Founded on valuable mathematical discoveries with a wide range of scientific applications, including the organic connection between probability theory and generating true random numbers.


Home | Search | New Writings | Fundamental Formula | Odds, Generator | Contents | Forums | Sitemap
