

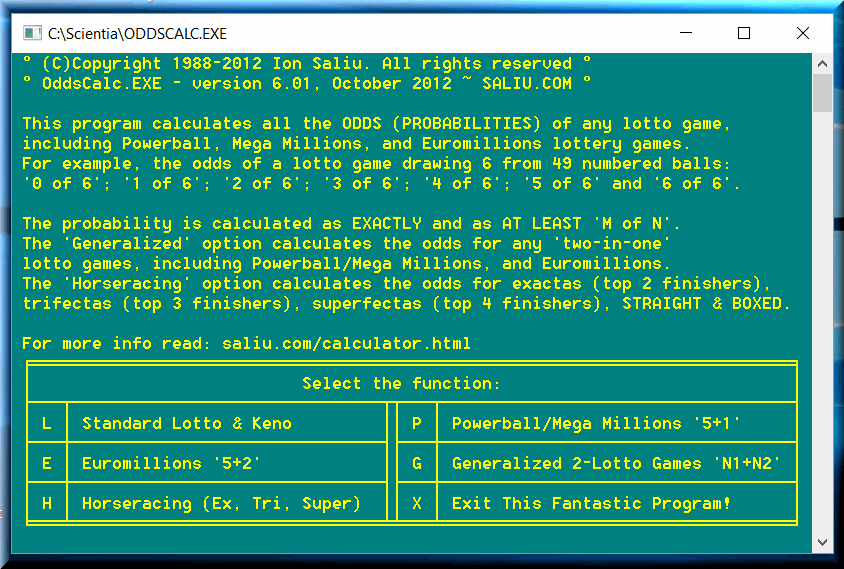
OddsCalc calculates the probabilities (odds) of any lotto game, including Powerball, Mega Millions, CA SuperLotto, Euromillions, Keno, and even horse racing. If the lotto game draws 6 winning numbers, the program calculates the odds from 0 of 6 to 6 of 6. Furthermore, the probability is calculated from two perspectives: as exactly and as at least.
The software calculates the lotto probability using the hypergeometric distribution probability. The odds are calculated as k of m in p from N. More clearly, let's suppose a lotto 6/49 game. The lottery draws 6 winning numbers. The player must play exactly 6 numbers per ticket. But the lottery player can choose to play a pool of 10 favorite lotto numbers. What is the probability to get 4 of 6 in 10 from 49? The odds: 1 in 90.
The general hypergeometric formula for the as exactly case:
The hypergeometric distribution probability formula has restrictions. Some cases are impossible; e.g. exactly 1 of 6 in 10 from 10.
My lotto software “runs” the extra mile and puts together multiple cases and does calculate precisely the odds as at least situations.
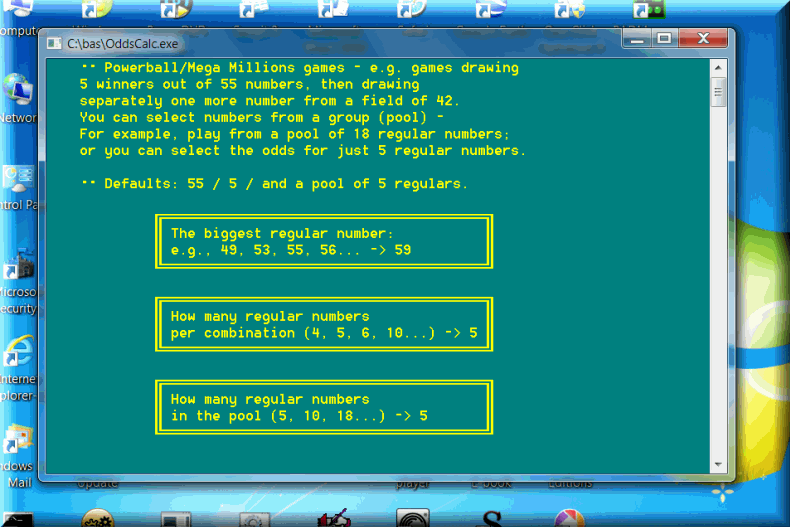
Again, there are situations when the players select pools of numbers which are larger than the amount of winning numbers drawn in the game. There are lottery syndicates that can afford to play 18 or 20-number pools. In fact, they asked me to calculate the odds for a lotto game in Australia that allowed the players to mark 20 numbers on their play-slips (instead of 6). Of course, that play requires huge amounts of money (there are 38760 lotto combosnations to play!) Nonetheless, this incredible lotto software can easily calculate the odds for all possible situations.
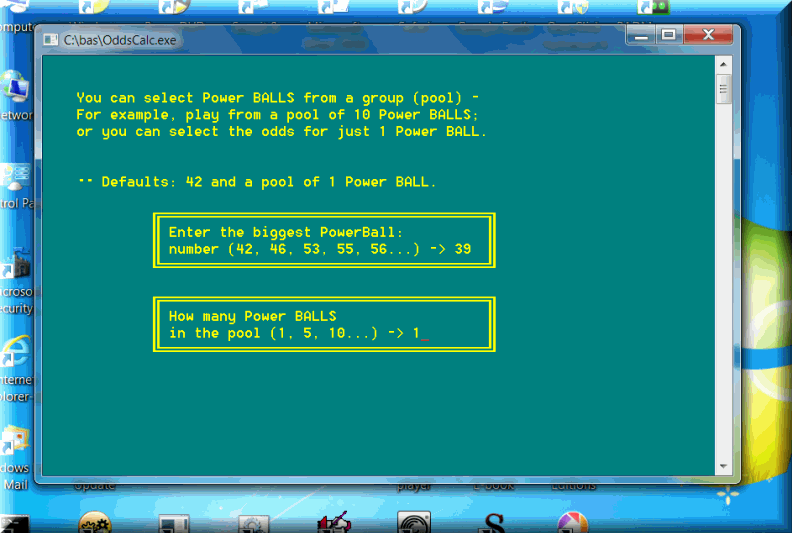
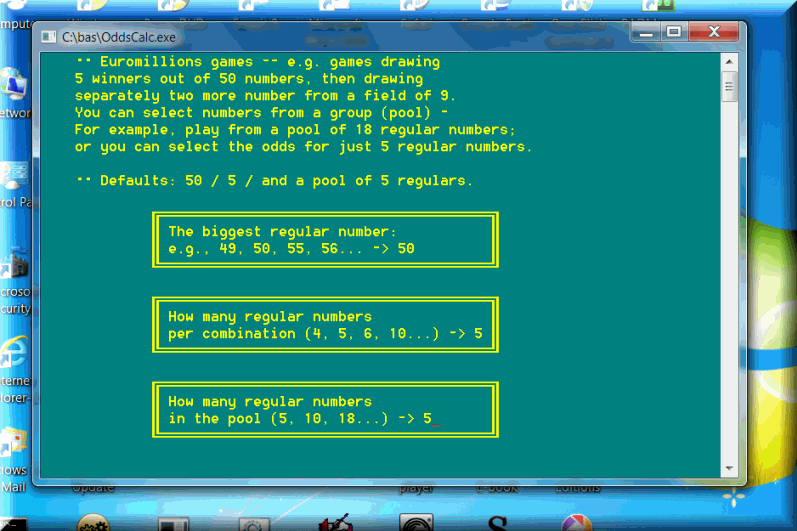
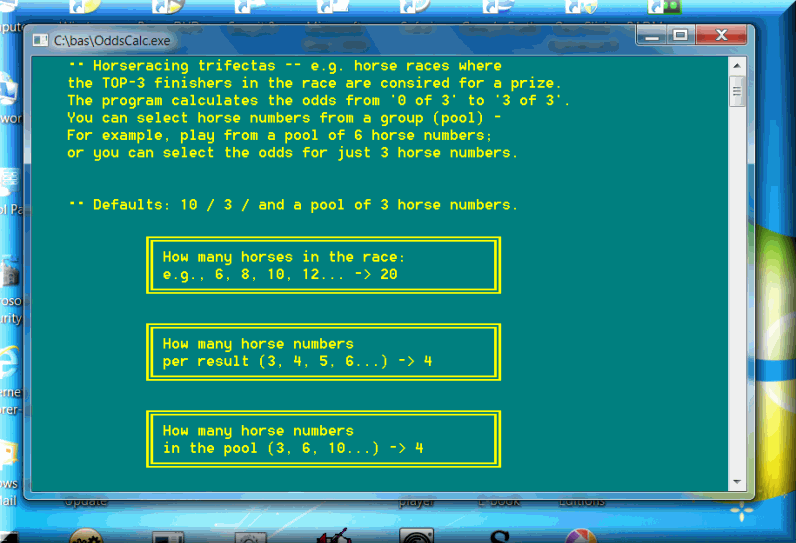
The program requires just a few parameters. They are easy to understand and explained in detail on the input screens. Say, you want to calculate all possible odds for a 6-49 lotto game, with no pool of extra numbers (i.e. calculate the odds for a 6-number pool, exactly the number of winning lotto numbers drawn by the lottery commission). The biggest lotto number: 49; How many lotto numbers per combination: 6; How many lotto numbers in the pool: 6.
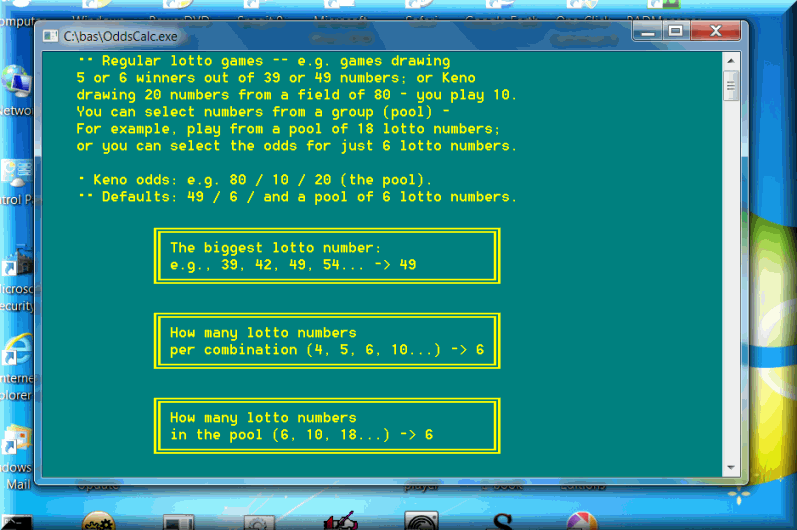
The calculations are saved to disk files only. All names start with Od; the text files can be opened in Notepad or any text editor. In this case: OdL49-6.6; easy mnemonics!
The odds calculated as EXACTLY in a lotto game '49/6/6': 0 of 6 in 6 from 49 = 1 in 2.29 1 of 6 in 6 from 49 = 1 in 2.42 2 of 6 in 6 from 49 = 1 in 7.55 3 of 6 in 6 from 49 = 1 in 56.66 4 of 6 in 6 from 49 = 1 in 1032.4 5 of 6 in 6 from 49 = 1 in 54200.84 6 of 6 in 6 from 49 = 1 in 13983816 The odds calculated as AT LEAST in a lotto game '49/6/6': 0 of 6 in 6 from 49 = 1 in 1 1 of 6 in 6 from 49 = 1 in 1.77 2 of 6 in 6 from 49 = 1 in 6.62 3 of 6 in 6 from 49 = 1 in 53.66 4 of 6 in 6 from 49 = 1 in 1013.03 5 of 6 in 6 from 49 = 1 in 53991.57 6 of 6 in 6 from 49 = 1 in 13983816
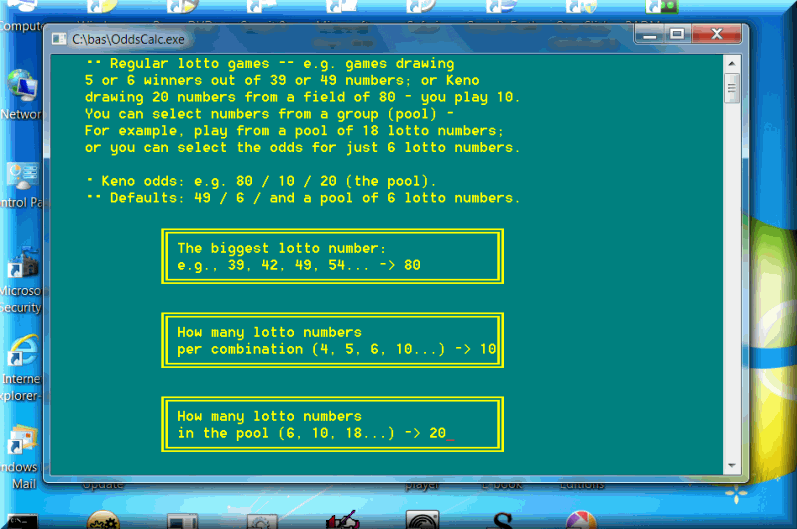
And here is that Tattslotto case when the players are allowed to mark 20 numbers on the playing cards: 45/6/20 (we never use the bonus numbers — bonus, bogus!)
The odds calculated as EXACTLY in a lotto game '45/6/20': 0 of 6 in 20 from 45 = 1 in 45.99 1 of 6 in 20 from 45 = 1 in 7.67 2 of 6 in 20 from 45 = 1 in 3.39 3 of 6 in 20 from 45 = 1 in 3.11 4 of 6 in 20 from 45 = 1 in 5.6 5 of 6 in 20 from 45 = 1 in 21.01 6 of 6 in 20 from 45 = 1 in 210.14 The odds calculated as AT LEAST in a lotto game '45/6/20': 0 of 6 in 20 from 45 = 1 in 1 1 of 6 in 20 from 45 = 1 in 1.02 2 of 6 in 20 from 45 = 1 in 1.18 3 of 6 in 20 from 45 = 1 in 1.81 4 of 6 in 20 from 45 = 1 in 4.33 5 of 6 in 20 from 45 = 1 in 19.1 6 of 6 in 20 from 45 = 1 in 210.14
The Keno odds are calculated by the same option: L = Standard Lotto and Keno. The parameters: 80/10/20 for the most common Keno format.
The odds calculated as EXACTLY in a lotto game '80/10/20': 0 of 10 in 20 from 80 = 1 in 21.84 1 of 10 in 20 from 80 = 1 in 5.57 2 of 10 in 20 from 80 = 1 in 3.39 3 of 10 in 20 from 80 = 1 in 3.74 4 of 10 in 20 from 80 = 1 in 6.79 5 of 10 in 20 from 80 = 1 in 19.44 6 of 10 in 20 from 80 = 1 in 87.11 7 of 10 in 20 from 80 = 1 in 620.68 8 of 10 in 20 from 80 = 1 in 7384.47 9 of 10 in 20 from 80 = 1 in 163381.37 10 of 10 in 20 from 80 = 1 in 8911711.18 The odds calculated as AT LEAST in a lotto game '80/10/20': 0 of 10 in 20 from 80 = 1 in 1 1 of 10 in 20 from 80 = 1 in 1.05 2 of 10 in 20 from 80 = 1 in 1.29 3 of 10 in 20 from 80 = 1 in 2.09 4 of 10 in 20 from 80 = 1 in 4.72 5 of 10 in 20 from 80 = 1 in 15.47 6 of 10 in 20 from 80 = 1 in 75.57 7 of 10 in 20 from 80 = 1 in 570.52 8 of 10 in 20 from 80 = 1 in 7059.54 9 of 10 in 20 from 80 = 1 in 160439.97 10 of 10 in 20 from 80 = 1 in 8911711.18
The odds calculated as EXACTLY in a Powerball game '59/5/5 AND 35/1/1': 0 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 1.63 0 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 55.41 1 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 3.26 1 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 110.81 2 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 20.78 2 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 706.43 3 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 360.14 3 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 12244.83 4 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 19087.53 4 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 648975.96 5 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 5153632.65 5 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 175223510 The odds calculated as AT LEAST in a Powerball game '59/5/5 AND 35/1/1': 0 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 1 0 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 35 1 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 2.72 1 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 95.03 2 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 19.06 2 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 667.21 3 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 343.35 3 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 12017.25 4 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 18473.75 4 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 646581.22 5 of 5 in 5 from 59 AND 0 of 1 in 1 from 35 = 1 in 5006386 5 of 5 in 5 from 59 AND 1 of 1 in 1 from 35 = 1 in 175223510

The odds calculated as EXACTLY in a Euromillions game '50/5/5 AND 11/2/2': 0 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 2.65 0 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 5.3 0 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 95.38 1 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 4.35 1 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 8.69 1 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 156.42 2 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 22.81 2 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 45.62 2 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 821.22 3 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 326.97 3 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 653.94 3 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 11770.89 4 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 14386.64 4 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 28773.28 4 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 517919.11 5 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 3236994.44 5 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 6473988.89 5 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 116531800 The odds calculated as AT LEAST in a Euromillions game '50/5/5 AND 11/2/2': 0 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 1 0 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 2.89 0 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 55 1 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 2.36 1 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 6.84 1 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 129.91 2 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 13.94 2 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 40.34 2 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 766.53 3 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 209.24 3 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 605.69 3 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 11508.18 4 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 9375.04 4 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 27138.29 4 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 515627.43 5 of 5 in 5 from 50 AND 0 of 2 in 2 from 11 = 1 in 2118760 5 of 5 in 5 from 50 AND 1 of 2 in 2 from 11 = 1 in 6133252.63 5 of 5 in 5 from 50 AND 2 of 2 in 2 from 11 = 1 in 116531800
1.a. The odds calculated as EXACTLY in horseracing - STRAIGHT bet '20/4/4': 0 of 4 in 4 from 20 = 1 in 63.89 1 of 4 in 4 from 20 = 1 in 207.64 2 of 4 in 4 from 20 = 1 in 969 3 of 4 in 4 from 20 = 1 in 7267.5 4 of 4 in 4 from 20 = 1 in 116280 1.b. The odds calculated as EXACTLY in horseracing - BOXED bet '20/4/4': 0 of 4 in 4 from 20 = 1 in 2.66 1 of 4 in 4 from 20 = 1 in 8.65 2 of 4 in 4 from 20 = 1 in 40.38 3 of 4 in 4 from 20 = 1 in 302.81 4 of 4 in 4 from 20 = 1 in 4845 2.a. The odds calculated as AT LEAST in horseracing - STRAIGHT bet '20/4/4': 0 of 4 in 4 from 20 = 1 in 46.2 1 of 4 in 4 from 20 = 1 in 166.83 2 of 4 in 4 from 20 = 1 in 848.76 3 of 4 in 4 from 20 = 1 in 6840 4 of 4 in 4 from 20 = 1 in 116280 2.b. The odds calculated as AT LEAST in horseracing - BOXED bet '20/4/4': 0 of 4 in 4 from 20 = 1 in 1.92 1 of 4 in 4 from 20 = 1 in 6.95 2 of 4 in 4 from 20 = 1 in 35.36 3 of 4 in 4 from 20 = 1 in 285 4 of 4 in 4 from 20 = 1 in 4845
In lotto games, however, the situations are much more complex. Therefore, the calculations are more complicated. Let's use a common example, as it refers to “the most famous lotto wheel in the world”: 49 numbers, 3 of 6 minimum guarantee, in 163 lines (combinations). That wheel guarantees at least 1 combonation with a 3 of 6 win — no denial about that. On the other hand, if we generate 163 random 6-number lotto combinations, we are NOT guaranteed to win 3 of 6 every time. In fact, if we randomly generate 13,983,816 combinations for a 6-49 lotto game, the degree of certainty to get the winning combination is 63.2%. The phenomenon is known as Ion Saliu's Paradox of N Trials.
Let's say we randomly generate 100 combinations for a 6-49 lotto game. What is the degree of certainty that none of the combinations will contain 3 or more winning numbers? In the first step, we run OddsCalc. The odds calculated as AT LEAST in a lotto game 49/6/6:
3 of 6 in 6 from 49 = 1 in 53.66;
In the next step, we need to run SuperFormula function M = At Most M successes in N trials. Parameters: 2 = The program calculates p, then 1, then 53.66, then 0, and then 100. We can see that the opposite of at least 3 of 6 is at most 3 of 6, 0 successes in 100 trials. That is, every combination in our 100-line block will register 0, or 1, or 2 winning lotto numbers — but NO 3 or more winners. Or, we can get the same result for 1 in 53.66 for exactly 0 successes in 100 trials. Either way, the lotto odds are 15.24% or 1 in 6.56 trials. We'll notice that, on average, we will not hit 3 or more winning numbers every 7 lottery drawings or so IF we play 100 random combinations.
Axiomatic ones, these calculations are valuable in conjunction with the LIE elimination function in my lotto software.
 Read Ion Saliu's first book in print: Probability Theory, Live!
Read Ion Saliu's first book in print: Probability Theory, Live!
~ Founded on valuable mathematical discoveries with a wide range of scientific applications, including precise calculations of odds, probability for every lotto game imaginable, including Powerball, Mega Millions, Euromillions.

